Anul trecut şcolar am avut două clase paralele de a 5-a, aşa încât eu personal am putut evolua de două ori mai mult în lecţiile specifice. În primele două părţi ale prezentului eseu am prezentat momentul “întâlnirii” elevilor cu fenomenul periodicităţii zecimale, cât şi mai ales toate gândurile pregătitoare necesare unui dascăl, astfel încât acest moment să fie unul de un impact cât mai puternic, dar totuşi cât mai pozitiv, accesibil şi nefrustrant pentru cât mai mulţi elevi.
Din păcate, în astfel de momente foarte mulţi profesori greşesc. Mentalul nostru general, cel puţin în România, după atâţia ani de zdroabă, împinşi fiind spre olimpiade şi excelenţă, mentalul nostru este focusat pe zona de aplicaţii cât mai complexe ale fiecărei lecţii. Majoritatea profesorilor “cu rezultate” neglijează inconştient începutul lecţiilor. Introducerea noilor noţiuni, itemi, lecţii este total neglijată. Unii “uită” să le facă, alţii le dau să fie copiate acasă din culegere sau mai rar din manual (şi acesta este un fenomen interesant ce ar merita discutat cu o ocazie); alţii îi pun în clasă să copieze lecţia dintr-o carte (cică metode noi – dacă a mers în pandemie, de ce n-ar merge şi acum?, iar profesoara are timp să stea puţin pe telefon). Alţii nu le predau, nu le dau nici ca temă, dar dacă copilul nu stă cuminte la oră este ridicat în picioare şi întrebat din noţiuni nepredate, la care desigur nu ştie şi deci primeşte un 2 (ca să se înveţe minte!).
Chiar şi în afară de astfel de forme extreme, totuşi, în general noi nu mai avem o cultură a introducerii noţiunilor noi la clasă. Fenomenul poate fi explicat şi astfel: tu, ca profesor, ai mai făcut lecţia asta de n-şpe ori; între timp, de la ultima trecere, eventual de anul trecut, ai găsit noi probleme şi de-abia aştepţi să le dai la clasă. Pe tine începutul lecţiei te plictiseşte profund. Doar că, în entuziasmul tău, tu uiţi cumva că aceştia sunt alţi elevi, că aceştia habar nu au despre lecţia respectivă (cel puţin cei cu care nu a parcurs nimeni lecţia în avans acasă! Acesta este un alt aspect ce ar merita tratat separat şi analizat pendelete.).
Da, într-adevăr, majoritatea profesorilor nu se concentrează pe o introducere “organică” a lecţiilor. Desigur că la acest fenomen a contribuit şi moda introducerilor definiţioniste a lecţiilor din anii ’80 ai secolului trecut, modă care nu a fost niciodată luată în discuţie şi în analiză la nivel naţional. Profesorul are impresia că odată date definiţia şi regulile, elevii le ştiu în mod natural şi înţeleg instant toată lecţia. Nimic mai greşit. În plus, profesorii au impresia că, odată prezentate principalele aspecte ale unei lecţii, elevii ştiu automat şi toate aspectele despre care nu s-a vorbit încă în lecţie.
Despre felul în care putem evita astfel de “gafe pedagogice” am încercat să vorbesc “printre rânduri” în primele două părţi ale eseului de faţă. Astfel, am încercat să arăt cum putem veni “din înaltul cerului nostru matematic” în întâmpinarea elevilor novice, cât mai jos, acolo unde se află aceştia înaintea predării lecţiei (încă o dată: asta dacă nu le-a arătat cineva cum stă treaba, dând astfel “spoil” la “filmul” ce urmează a fi vizionat).
Eu, ca profesor, trebuie “să mă cobor acolo jos unde este elevul” (elevul mijlociu), adică să pornesc lecţia mea de la lucruri pe care majoritatea elevilor le ştiu deja bine şi să urc pe o pantă destul de lină, adaptată majorităţii, astfel încât să am siguranţa că “nu pierd pe drum prea mulţi puiuţi”. Lecţia astfel ar trebui structurată încât orice elev binevoitor să meargă cu lucrurile înţelese acasă (bine înţelese şi deja parţial fixate). Aşa se preda pe vremuri (până prin anii ’70) şi până la un anumit nivel al lecţiilor majoritatea elevilor de la toate nivelele nu aveau nevoie de explicaţii suplimentare acasă, nici vorbă de meditaţii regulate (cel puţin nu cei de la mediu în sus, cel puţin nu la o astfel de lecţie cu abilităţi de bază cum este algoritmul împărţirii). Tema de casă trebuie apoi să repete măcar parţial cele întâmplate la oră, astfel încât aceste abilităţi şi cunoştinţe să se fixeze bine.
Nu vreau să susţin că lecţiile de introducere ar trebui să dureze foarte mult, dar nici prea puţin sau defel. Profesorul trebuie să le adapteze la nivelul clasei. La o clasă bună, selectată, lecţia precedentă ar putea să dureze cel mult 15 min. Dimpotrivă, la o clasă ce are şi copii mai slabi la matematică, acestora trebuie să li se acorde mai mult timp pentru digerarea noilor situaţii.
Setul de exemple de împărţiri prezentat în prima parte este suficient de bogat în diversitatea formelor rezultatelor, acesta trebuind repetat şi la temă (desigur cu alte exemple, poate mai multe exerciţii, dar şi eventual amestecate cu câteva fracţii zecimale finite). În altă ordine de idei, sper că s-a observat faptul că setul propus spre parcurgere la clasă este totuşi destul de scurt (cum am spus, la elevii buni probabil până în 10-15 min.). Revin, precizând că acest aspect a fost intenţionat gândit ca atare: pentru elevii slabi o astfel de lecţie este suficientă pentru o oră (la aceştia munca va dura mult mai mult decât la cei buni), putând fi eventual pornită la clasă şi tema pentru casă (aşa sunt de fericiţi când au ocazia să pornească tema la clasă! Cei mai mulţi nu apucă să facă tare mult în ultimele 3-5 minute, dar sunt atât de recunoscători de ideea că tema a scăzut, încât pleacă toţi fericiţi de la ora de mate). Pentru elevii buni, desigur că o astfel de lecţie scurtă lasă loc şi pentru aplicaţii mai grele, atât la începutul orei (deci din lecţiile precedente), cât şi după (deci din lecţia de faţă).
Să revenim însă la fracţiile noastre periodice: mai avem de studiat şi drumul invers, adică transformarea fracţiilor zecimale periodice înapoi în fracţii ordinare. Elevii cunosc cumva ideea de la fracţiile zecimale finite, unde au cunoscut deja ambele direcţii de transformare şi unde am accentuat asupra faptului că fracţiile au două forme de manifestare, două “limbi de exprimare” şi că noi putem să transformăm o anumită fracţie şi într-o direcţie şi în cealaltă.
Apropos de fracţiile zecimale finite: aici apare un fenomen foarte ciudat din punct de vedere a felului în care văd profesorii o noţiune, o lecţie, un fenomen matematic, pe de-o parte, şi felul în care acesta este văzut de elevii aflaţi în procesul cunoaşterii. Daţi-mi voie să evidenţiez acest fenomen pe exemplul fracţiilor zecimale finite, deşi fenomenul este prezent şi în multe alte locuri.
Fracţiile zecimale apar de la împărţirea numerelor şi nu este normal să îi confruntăm “din prima” pe elevi cu situaţia periodicităţii (aici toată lumea este cumva de acord). Incluzând însă în titlu cuvântul finite, putem genera una din următoarele două situaţii: fie îi derutăm pur şi simplu pe cei mai mulţi, fie dăm “spoil” la ce urmează, adică stricăm surpriza lecţiei următoare, eventual cauzând la elevii mai curioşi impulsul să studieze în avans (pe internet sau întrebând un părinte). Părerea mea este că cel mai des se va întâmpla prima situaţie (că dacă s-ar întâmpla prea destul des a doua situaţie, măcar am ştii că le-am stârnit curiozitatea şi asta tot ar fi bine). Rămânând la prima variantă, uneori chiar am impresia că profesorii asta îşi şi doresc: să-i bulverseze pe elevi (şi de aici am putea să divagăm spre un fenomen ce a ajuns să se manifeste la nivel naţional).
Vorbim aici deci de fenomenul folosirii unor cuvinte sau expresii pe care elevii încă nu au de unde să le ştie, dar pe care programa oficială le impune la un anumit moment. Dar unde mai apare acest fenomen? Păi. să vă dau nişte exemple la întâmplare. Folosirea termenului de număr raţional pozitiv înaintea cunoaşterii numerelor negative va trezi în orice minte ageră curiozitatea despe ce şi cum. Dimpotrivă, folosirea termenului coplanare în definiţia dreptelor paralele din clasa a 6-a va bulversa masiv înţelegerea copilului obişnuit. Mai sus, în a 8-a sau a 9-a, apare un astfel de moment când discriminantul unei ecuaţii de gradul II este negativ şi nu spunem pur şi simplu că ecuaţia nu are soluţii în acest caz, ci ne simţim toţi datori să le precizăm că nu are soluţii reale. Întotdeauna de aici se iscă întrebarea: dar există şi alte numere pe lângă cele reale?
Există şi un exemplu de folosire a unei expresii legată de “ceva” ce însă nu va veni nici pe viitor, conform programei, iar asta o pot descrie ca “răutatea supremă”. Vorbesc aici despre folosirea denumirii de prismă dreaptă cu baza pătrat, ce se întâlneşte foarte des prin cărţi. Descriu asta drept o răutat pentru că elevii nu învaţă dualitatea prismă dreaptă – prismă oblică, dar nici măcar ideea de prismă dreaptă, care ar necesita desigur măcar un exemplu (de pildă o prismă dreaptă cu baza un romb, pe care calculele sunt foarte uşoare). Este evident că dacă ar fi incluse şi acestea în programă. s-ar năpusti toţi olimpiştii în acea zonă. Acestea au fost exluse din materie la începutul anilor ’90, aşa că nici expresii ce ţin de ele nu ar avea voie să apară prin cărţi.
De ce trebuie să le facem asta constant elevilor noştri, această înjosire constantă, prin care să le arătăm sistematic că ei nu ştiu destul? Haideţi să facem un experiment cu dvs., profesori de matematică ce aveţi pretenţia că ştiţi desigur totul despre matematica preuniversitară. Cum vă simţiţi la următoarea afirmaţie: numerele iraţionale de tipul radical din 2 sau radical din 3 etc. au o formă infinită neperiodică, dar asta doar în sistemul de scriere zecimal. Cum adică? Există o altă formă de scriere a acestor numere care este infinită dar periodică?, veţi întreba. Iar eu voi răspunde că Da!, există, doar că dvs. încă n-aţi învăţat-o. Iar acum schimb subiectul, pentru că nu ne-am propus să vorbim aici despre fracţiile continue.
Revenind la fracţiile zecimale finite, după părerea mea acestea pot fi denumite oficial de-abia după cunoaşterea fracţiilor periodice. În acest sens putem face o scurtă sistematizare la sfârşitul orei respective (dacă mai este timp suficient), sau putem să o aducem ca o formă de reactualizare la începutul orei următoare (aşa este poate chiar mai bine). Ca o paranteză pentru pedanţi, experienţa îmi arată că nu apar întrebări de genul: dar există şi fracţii infinite neperiodice? Totuşi, dacă ar apărea această întrebare, le-aş răspunde calm că da, sunt radicalii (de care elevii au cam auzit, că-i văd pe calculatoarele de pe telefoane), doar că despre aceştia vom învăţa prin clasa a 7-a pentru că sunt ceva mai complicaţi.
Înainte de a vorbi despre transformarea fracţiilor periodice în fracţii ordinare mai trebuie să prezint un scurt aspect ce ţine de didactica predării. Eu personal mă străduiesc cât se poate de mult să le aduc elevilor noile cunoştinţe în forme pe care ei să le înţeleagă de unde vin. Când predau prin întrebări (prin problematizare etc.) este evident că elevul care dă răspunsul corect a intuit de unde vine ideea. Chiar şi acolo unde nu pot să-i îndrum pe elevi pe o cale de descoperire, le explic eu cum se face, dar mă străduiesc să le-o prezint astfel încât să le generez o cât mai clară senzaţie de înţelegere a raţionamentului sursă al fenomenului respectiv. Înţelegând raţionamentul care duce la o nouă situaţie, elevul îşi formează totodată şi gândirea. Predând cât mai des astfel încât elevii să înţeleagă sursa logică a noţiunilor, eu am certitudinea şi bucuria că pot contribui constant la formarea unei gândiri raţionale la elevi.
Totuşi, există situaţii când uneori chiar nu le putem explica nicicum de unde vine ideea, cel puţin nu la nivelul la care sunt elevii în acel moment (algoritmul de extragere a rădăcinii pătrate este o astfel de situaţie; chiar aşa, ştiţi cum se justifică acesta? Întrebarea asta a venit în contextul în care am vorbit de înjosirea celorlalţi; Scuze că folosesc asta pe dvs.).
Pentru că elevii trăiesc constant strădania mea de a-i face să înţeleagă, într-un asfel de moment beneficiez de un soi de “clemenţă” din partea lor atunci când le spun: aici nu am cum să vă explic de unde vine; aici pot doar să vă arăt cum se face. Aici pot să fac doar ca toţi ceilalţi din breasla mea; dacă-mi aduceţi aminte peste doi ani, atunci vă voi putea explica de ce se face aşa. Un astfel de moment este şi la transformarea fracţiilor zecimale periodice în fracţii ordinare.
Faptul că transformarea se face într-o fracţie cu numitorul format din atâţia de 9 câte cifre erau în perioadă, acesta este un fapt ce are un efect tranchilizant, de anestezie totală asupra gândirii învăţăcelului. De unde 99 la o fracţie de tipul 0,(37)? Regula se înţelege destul de uşor; de pild la 0,(375) vom scrie automat numitorul 999. Dar de ce? DE CE?
Trecând peste acest moment de neînţelegere “că de ce se face aşa?”, elevii nu au mari probleme în a aplica noua regulă în cazurile simple. Cumva ţine însă de arta profesorului “să le facem viaţa cât mai uşoară” şi să le prelungim cât mai mult starea de “cazuri simple”, adică să nu-i trecem prea repede la “cazuri complicate”.
Pentru a prelungi starea de “caz simplu”, eu le dau forma de fracţii zecimale periodice simple supraunitare prin trecere în scriere cu întregi ca fracţie ordinară. Concret, odată ce a înţeles primele cazuri (cele de mai sus, pe câteva exemple), eu le dau modele de felul 3,(45) = 3 întregi şi 45/99 (scuzaţi scrierea, vreau să am garanţia că se poate citi de orice aparat). Astfel şi acest caz este unul simplu, aducând doar combinaţia noii reguli cu forma mai veche, uşor de reamintit, ce necesită apoi doar introducerea întregilor în fracţie (o bună ocazie de reactualizare).
De-abia la forma fracţiilor periodice mixte vin cu varianta ce implică scădere, simultan cu numitorul ca o combinaţie de 9 şi de 0. De pildă 0,4(25) = (425 – 4)/990. De ce se întâmplă aşa, asta este din nou o mare enigmă pe care nu le-o putem explica acum elevilor. Ce putem însă este ca la forma din aliniatul precedent să nu le-o băgăm încă (aşa cum din păcate s-a stabilizat la ora actuală în toate manualele şî auxiliarele). Evident că lecţia urmează să primească cât mai multe exerciţii, dar aici eu nu mai continui pentru că acestea se găsesc peste tot în cantităţi suficiente.
Legat de exerciţii, am un singur “contra-exemplu”, anume o hiper-capcană pentru elevi găsită într-o culegere (seria condusă de dl. profesor Artur Bălăucă, la ed. Taida). Fracţia zecimală periodică mixtă 1,0(6) este cuprinsă într-un exerciţiu cu mai multe operaţii, inclusiv paranteze (direct paranteze drepte, pentru că cele rotunde sunt rezervate pentru perioade). De ce este acesta o hiper-capcană? Pentru că elevul a fost împins pe calea unei rezolvări care permite apoi o capcană. Rezolvarea cu scrierea întregilor, sugerată mai sus, nu ar împinge elevul spre această greşeală. Despre ce este vorba? Aplicând rezolvarea propovăduită actualmente de toată lumea, elevul va avea tendinţa să neglijeze acel zero şi să scrie 106 – 1 la numărător, şi nu 106 – 10. Pe această capcană o mai putem numi şi “mină anti-elev”.
O altă problemă ce implică aspectele metodico-didactice ale acestei lecţii o reprezintă forma în care le dăm aceste reguli elevilor. Din păcate, majoritatea profesorilor şi majoritatea cărţilor prezintă aceste reguli într-o formă scrisă cu litere în loc de cifre, având astfel pretenţia că devine generală. Din păcate marea majoritate a elevilor nu înţeleg NIMIC din aceste scrieri, dar NIMIC-NIMIC! Realitatea acestei predări e ca şi cum acele sfaturi din startul Programei de gimnaziu din 2017 despre o predare cât mai întuitivă, cel puţin la clasele gimnaziale mici, sunt de fapt aplicate exact pe dos. Aici o predare intuitivă înseamnă să-i dai câteva exemple cât mai sugestive, iar elevul prin simpla imitaţie să facă mai departe alte şi alte exerciţii similare în acelaşî fel. Atâta tot! Cei mai mulţi le vor înţelege imediat, iar cei care nu le înţeleg nici aşa, “asta e!”. Cei mai slabi oricum nu le vor înţelege nici din forma generală dată prin litere. Dând însă aceste reguli prin exemple, creştem considerabil numărul elevilor ce le vor înţelege şi le vor putea face fără ajutor de acasă.
Din forma cu litere însă, “marea mare” majoritate nu vor înţelege nimic şi vor avea deci nevoie de explicaţii reluate acasă. Iar acasă, fie un părinte, fie un meditator plătit le va prezenta câteva exemple şi gata: elevul va înţelege.
E aşa de simplu cu exemple. Dar de ce să le prezinte profesorii lucrurile simplu elevilor, când pot să le facă viaţa grea şi amară la orele de matematică? Această atitudine mi se pare stupidă, chiar profund încărcată de o adevărată răutate. Îmi pare rău pentru agresivitatea acestor rânduri, dar aşa se văd lucrurile din punctul meu de vedere.
După părerea mea şase exemple lămuresc cu totul situţiile de aici. Gândind acum, eu le-aş aranja astfel: pe coloana din stânga trei exemple subunitare cu perioadă de una, doua respectiv trei cifre, măcar una sau două care să se simplifice, iar pe coloana din dreapta o fracţie supraunitară dar cu partea zecimală simplu periodică, apoi una subunitară mixtă (deci fără întregi), cât şi una supraunitară mixtă (deci cu întregi). La ultimele două trebuie să aleg diferit numărul de cifre din perioadă şi cel de cifre dintre virgulă şi perioadă, pentru a da impresia de situaţie generală.
Ajută la aceste exemple dacă folosim puţină culoare pentru a conecta vizual de pildă numărul de cifre din perioadă cu numărul de 9 de la numitor. Desigur că merită adăugate înaintea acestui set şi unul-două exemple de transformare de fracţii zecimale finite, care implică un 1 şi atâia de 0 la numitor câte cifre erau în partea zecimală. Două culori diferite vor ajuta elevii să conecteze exact aşa cum trebuie cele întâmplate.
Am convingerea că un set bine ales de astfel de exemple este mult mai clar pentru oricine decât nişte forme artificiale de reguli cu litere, sau o descriere în text (atunci când, pe lângă linia de fracţie, mai apare şi bara de deasupra, pentru scrierea în baza 10, cei mai mulţi elevi “cad pe spate, ca gândacii” şi “dau neajutoraţi din mâini şi din picioare!”). Îmi cer încă o dată scuze, dar chiar nu se gândeşte nimeni la aspectele acestea?
Haideţi să încheiem totuşi într-o notă pozitivă: deci, cum se poate demonstra la nivelul unor elevi de clasa a 7-a să zicem, sau a 8-a, de ce are loc transformarea în fracţie ordinară cu numitorul atâţia de 9 câte cifre erau în perioadă? Şi ca să fiu cât se poate de clar, vă voi face prezentarea exact în formatul unui exemplu numeric, situaţie ce acţionează deosebit de intuitiv la orice om, şi la noi, la profesori, dar şi la elevi.
Să alegem de pildă numărul 0,(375) pe care îl şi notăm cu a = 0, (375). Să înmulţim această egalitate cu 1000 şi obţinem 1000a = 375,(375). Scăzând prima egalitate din a doua obţinem 999a = 375 de unde deducem imediat că a = 375/999 (scrieţi dvs. pe hârtie varianta obişnuită, cu linie de fracţie). Asta a fost. E simplu pentu un elv de a 7-a, a 8-a. Poate ar merge şi în a 6-a, dar sigur marea majoritate nu o vor înţelege în finalul clasei a 5-a. Eu am găsit această “demonstraţie” într-o culegere veche din 1970 de pregătire a examenului de admitere în licee, deci pentru recapitularea din clasa a 8-a a materiei de clasele 5-8. Nu mai găsesc culegerea respectivă (cine ştie în ce cutie am pus-o), dar ştiu că pe copertă era ca nume dominant Ivanca Olivotto (m-a surprins pentru că la vremea respectivă, profesor tânăr fiind, nu-i ştiam istoricul şi cunoşteam doar culegerea de aritmetică cu acest nume).
Precizez un aspect important: chiar dacă un profesor ar avea impresia că aceste artificii de calcul într-adevăr pot fi înţelese de către elevi şi s-ar gândi să le arate elevilor în clasa a 5-a, realitatea ar avea şanse mari să fie una opusă. Haideţi să analizăm puţin lucrurile din punct de vedere a fenomenului dilemei cognitive. Elevii tocmai ce au fost confruntaţi cu o puternică dilemă cognitivă. În aceste condiţii lămurirea şi justificarea respectivei dileme cognitive ar trebui să aibă loc pe o cale cognitivă care face deja parte din uzualul elevilor, din “zona lor de confort” intelectual. Or, astfel de artificii sigur încă nu fac parte din zona de confort calculaţionist al elevilor obişnuiţi în clasa a 5-a. Făcând această “demonstraţie” la clasă, pentru cei 2-3 vârfuri ai colectivului, asta îi va bulversa şi mai mult pe toţi ceilalţi, împingându-i din nou spre învăţat pe de rost şi spre meditaţii private. Dimpotrivă, la o grupă de excelenţă, acolo s-ar putea face liniştit.
Tot în acea lucrare am găsit şi o “demonstraţie” foarte accesibilă a criteriului de divizibilitate cu 9, fapt ce întăreşte ideea că la clasele mici le putem da anumite reguli nejustificate, dar că odată ce elevii evoluează pe scara gândirii, noi ar trebui să venim cu o reluare mai matură în timpul căreia să aducem şi astfel de completări. Din păcate, nici în a 7-a şi sigur nici în a 8-a nu are nimeni timp pentru astfel de “filozofii”, acolo toată lumea fiind focusată pe “doparea” elevilor cu problemele şi situaţiile specifice verificate în examen (nimeni nu te întreabă la EN dacă cunoşti de ce se scrie cu 999 la numitor).
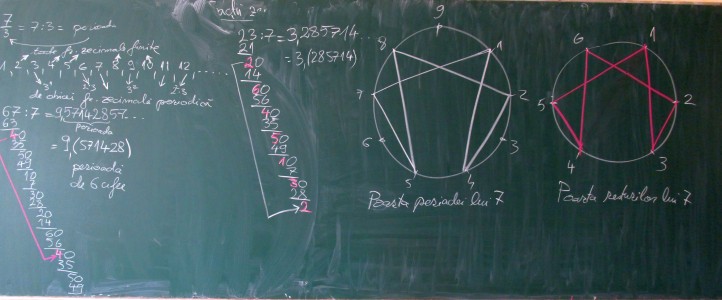
Da, cam astfel de gânduri ar trebui să avem noi atunci când venim cu “o lecţie banală” în clasă. Pentru mine gândurile pregătioare urmăresc un astfel de evantai de aspecte diverse, dar profund interconectate între ele. Nu poţi doar să turui o lecţie cât mai teoretic şi scurt, iar apoi să te plângi că elevii “n-au învăţat acasă”. Într-o lecţie de matematică trebuie pus mult suflet. Eu. doar aşa ştiu să fac. Închei cu câteva poze de tablă de la lecţiile din anul şcolar precedent, din care se poate obţine o oarecare impresie despre aspectele prezentate. C.Titus Grigorovici
P.S. Starea de îngâmfare, acea renumită stare de “eu ŞTIU!” este foarte periculoasă. Noi trebuie să fim conştienţi de acest aspect şi constant treji împotriva ei. De pildă, acum în final, recitind tot articolul şi aruncând o ultimă privire asupra celor două poze, mi-am dat seama de o mică gafă. În ultimele pagini am propovăduit calea transformării fracţiilor zecimale supraunitare în fracţii ordinare cu întregii scrişi separat, dar în pozele respective eu n-am dat nici măcar un exemplu similar în cazul fracţiilor zecimale finite. De pildă, la recapitularea dinaintea transformării fracţiilor periodice eu ar trebui să dau măcar un exemplu de transformare de felul: 3,65 = 3 întregi şi 65/100 care apoi să fie transformat prin introducerea întregilor în fracţie în (3 · 100 + 65)/100 = 365/100. Da, da! Cât trăim învăţăm.