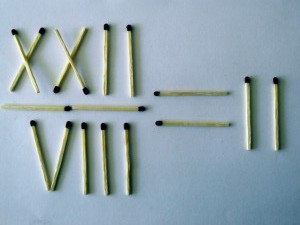Un elev de clasa a VIII-a m-a atenţionat de curând asupra acestei emisiuni, găsită pe net. Am căutat scamschool, am intrat pe Scam School / Test Tube şi am găsit (printre multe alte nebunii) câteva probleme foarte drăguţe de matematică distractivă (mathematical puzzles). Emisiunea este prezentată într-un mod foarte atractiv/agitat de către Brian Brushwood şi la majoritatea episoadelor este vorba de un pariu, anume cine plăteşte berea.
Totuşi, cred că mai există şi un alt motiv – în afară de berea din timpul emisiunii – pentru care partenerii de discuţie ai lui Brian sunt de peste 20 ani, chiar şi până în 40. Oare care ar fi acest motiv? Pentru că problemele sunt tehnic, prin prisma rezolvărilor, la nivel de gimnaziu (în general de clasa a 5-a). Haideţi să vedem câteva dintre aceste probleme (am căutat din emisiunile ultimului an). Interesant este că unele dintre ele permit mai multe soluţii. Le prezint pe fiecare cu titlul original al episodului respectiv:
The Most Powerful Number Puzzle. Se dau toate cifrele 0 1 2 3 4 5 6 7 8 9 = 1. Aveţi voie să puneţi orice semne sau operaţii din matematică, dar să păstraţi ordinea cifrelor (de la stânga la dreapta), şi trebuie să obţineţi rezultatul 1. Se caută desigur cea mai elegantă soluţie.
Fill in the Blanks: A Number Puzzle. Trebuie scrise trei numere a căror sumă să dea 30, adică ___ + ___ + ___ = 30 folosind ca piese de lucru doar unele din următoarele numere: 1, 3, 5, 7, 9, 11, 13, 15. La acesta Brian a trebuit să plătească el berea, pentru că prietenii lui au găsit o altă soluţie decât a sa, dar la fel de frumoasă. Un elev din a VII-a a găsit la prima prezentare, în 3-4 minute, altă soluţie decât cele două din emisiune.
The Toothpick Variable. Această problemă cu scobitori cere să stabiliţi egalitatea mutând doar o singură scobitoare în membrul stâng, pentru a obţine într-adevăr numărul patru (în membrul drept este 4 pe sistemul roman vechi: IIII, nu IV):
CRUSH Smug Geniuses With The Simplest Number Puzzle. În această problemă se primesc câteva bileţele pe care trebuie să le ordonaţi pentru a obţine rezultatul 24 (bileţelele =, 2 şi 4 sunt fixe). Atenţie că şi aici am găsit mai multe soluţii (daţi problema la elevi într-o pauză şi veţi vedea ce iese).
Single Digit FACE-OFF. Se cere ca folosind un calculator de buzunar să obţineţi numărul 17 apăsând doar cifra 5 şi orice/oricâte operaţii doriţi. Desigur că sunt căutate soluţii cât mai frumoase, adică cu cât mai puţine folosiri ale tastei 5. În filmuleţ apar soluţii cu şapte de 5, cu şase de 5, cu cinci de 5, chiar şi cu patru de 5, dar cireaşa de pe tort este o variantă în care se apasă tasta 5 o singură dată, iar în rest doar taste de operaţii.
Match Math. Un ultim exemplu este cu chibrite (chibrite, scobitori, ce gasiţi). Scrieţi cu chibrite “egalitatea” VII = I. Sarcina este să mutaţi un chibrit în partea stângă a semnului egal pentru a obţine într-adevăr rezultatul 1.
Morala poveştii: Pe vremuri, Martin Gardner publica în Scientific American probleme de matematică distractivă, câte una pe revistă. Răspunsul apărea de-abia în următorul număr al revistei. Această politică îţi lăsa chiar timp ca să te gândeşti şi să cauţi tu o soluţie. Ori, în emisiunile de pe Scam School totul decurge foarte repede şi, în avântul emisiunii, primeşti şi răspunsul în 2-3 minute. Astfel eşti redus la un simplu spectator la SPECTACOLUL GÂNDIRII.
Eu consider că rolul nostru ca profesori de matematică este să-i atragem pe elevi să fie activi în acest proces al gândirii, nu să se uite pasiv, din exterior, la cineva care gândeşte. Astfel, eu le dau elevilor problemuţe din acestea şi îi las să gândească (câteva minute, sau rămâne ca temă). Şi, în general, chiar careva reuşeşte de obicei să găsească o soluţie valabilă. Cât despre numele site-ului respectiv, nu l-am dat la clase ca să nu se uite şi să găsească acolo răspunsurile, rămânând să gestionez eu situaţia, când şi cum le dau răspunsul.
Constantin Titus Grigorovici






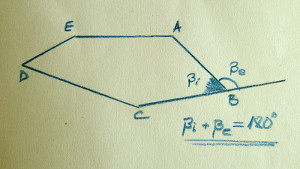
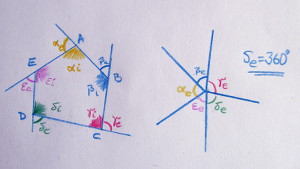


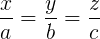 .
.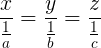 .
.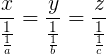 ,
,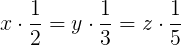 ,
,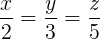 .
.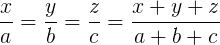 .
.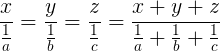 .
.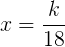 ,
, 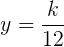 şi
şi 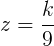 .
.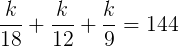 . După o scurtă muncă de rezolvare a acestei ecuaţii obţinem k = 576, iar apoi imediat: x = 32, y = 48 şi z = 64 bombonele (cel mic trebuie să primească cele mai multe bombonele, pe când cel mai mare, cele mai puţine; logic, nu?).
. După o scurtă muncă de rezolvare a acestei ecuaţii obţinem k = 576, iar apoi imediat: x = 32, y = 48 şi z = 64 bombonele (cel mic trebuie să primească cele mai multe bombonele, pe când cel mai mare, cele mai puţine; logic, nu?).