În toamna anului 1982 eram în clasa a X-a. La o oră de matematică mama mea, care ne era profesoară, a adus la oră şi câteva probleme cu trapeze. După primele două probleme destul de accesibile a venit o a treia care ne-a lovit puternic. Un alt coleg a fost la tablă, aşa că am putut gândi liber. Deşi am relatat de nenumărate ori ce a urmat, acum este prima oară când “aştern pe hârtie” povestea acelei întâmplări memorabile.
Pe scurt, în următoarele minute am descoperit o nouă “formulă pentru aria triunghiului”, o reţetă necunoscută până în acel moment; nici un profesor nu o cunoştea şi aceasta nu se găseşte în nici o carte. În ora respectivă mintea mea a umblat pe unde nu a mai umblat nici o minte de om. Descoperisem “o mică pată albă” pe întinsa hartă a matematicii, iar aceasta nici măcar nu era la periferie, ci se afla în zona centrală, elementară a matematicii, zona pentru elevi.
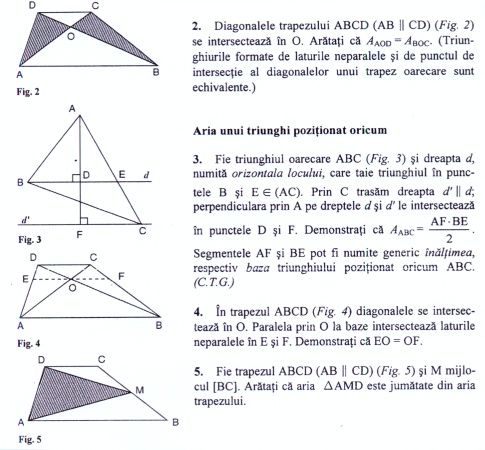
Iată în continuare cele trei probleme şi evoluţia gândurilor mele din acea oră.
- Fie trapezul oarecare ABCD cu AB || CD şi O punctul de intersecţie al diagonalelor. Demonstraţi că ΔAOD şi ΔBOC au aceaşi arie (sunt echivalente).
- În trapezul oarecare ABCD alegem M mijlocul laturii oblice [AD]. Demonstraţi că AriaΔMBC = ½ ∙ AriaABCD.
- Prin punctul O de intersecţie al diagonalelor unui trapez trasăm o paralelă la baze, aceasta intersectând laturile oblice în punctele E respectiv F. Demonstraţi că O este mijlocul segmentului [EF].
Imaginea prezentată este o scanare din culegerea De la Cercul lui Thales la Moneda lui Ţiţeica, C. Titus Grigorovici, Mariana Grigorovici, publicată în 2006 la Humanitas Educaţional. În culegere am schimbat ordinea problemelor faţă de cea din ora respectivă.
După cum am spus, demonstraţiile primelor două probleme mi s-au părut accesibile; chiar am avut atunci o senzaţie de frumos în acele momente, probabil şi datorită faptului că reprezentau o îmbinare de geometrie şi algebră.
1) Având aceaşi bază şi înălţimile egale, ΔADC şi ΔBDC au aceeaşi arie. Din egalitatea celor două scădem porţiunea comună, aria ΔODC, obţinănd egalitatea ariilor ΔAOD şi ΔBOC. Nu am în amintire cum s-a scris rezolvarea pe tablă, dar ştiu cum am scris-o eu:
2) Trasând linia mijlocie [MN] observăm că ΔBMN şi ΔCMN au aceeaşi arie, având baza comună şi înălţimile egale (cât jumătate din înălţimea trapezului). Obţinem astfel:
AriaΔMBC = AriaΔBMN + AriaΔCMN =
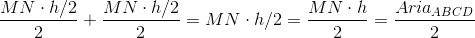
3) La a treia problemă lucrurile nu arătau deloc la fel de frumos, în primul rând pentru că rezolvarea previzibilă era cu asemănare de triunghiuri; era o rezolvare lungă şi istovitoare. Nu aveam nici un chef de aşa ceva; se prevedea o demonstraţie urâtă în comparaţie cu precedentele. Ei, şi atunci mintea mea a început să lucreze, observând anumite coincidenţe:
– triunghiurile echivalente din prima problemă apăreau şi aici;
– cele două triunghiuri echivalente stăteau ambele înclinate, într-un colţ; la fel şi triunghiul MBC din problema a doua (triunghiurile stau de obicei pe bază, nu înclinat);
– triunghiul MBC din a doua problemă are aria egală cu semiprodusul “orizontalei” prin M cu înălţimea totală a triunghiului, adică “diferenţa de nivel” între B şi C;
– cele două triunghiuri echivalente din prima problemă au aceeaşi înălţime totală, adică “diferenţa de nivel” între vârful de la baza mică şi cel de la baza mare a trapezului, iar cerinţa spune că “orizontalele” prin vârful intermediar ar trebui să fie egale;
– avem deci trei mărimi care se pare că depind una de cealaltă: aria unui astfel de “triunghi răsturnat”, apoi “înălţimea totală” a triunghiului, adică “diferenţa de nivel” între vârful situat cel mai jos şi vârful situat cel mai sus, iar pe post de bază “orizontala” prin punctul intermediar până la latura opusă.
Dacă reuşeam să demonstrez că aria unui triunghi ce este poziţionat înclinat, adică neavând baza aliniată pe “orizontala” figurii, aria unui astfel de triunghi respectă modelul tradiţional de baza ori înălţimea pe doi, atunci era rezolvată problema 3). De aici lucrurile au mers uşor: mi-am făcut o figură separată pentru “teorema” ce-o doream demonstrată, am descompus triunghiul mare în două pe baza “orizontalei”, m-am jucat puţin cu factorul comun şi VOILA!, gata era teorema mea.
Desigur, rezolvarea mea era mai scurtă şi datorită faptului că fentasem, folosind rezultatul primei probleme drept cunoscut. Oricum însă, terminasem cu câteva minute bune înaintea colegului de la tablă, care se chinuia împreună cu maică-mea printre rapoarte şi triunghiuri asemenea. Iar eu eram literalmente în al nouălea cer, având în plus şi o teoremă şmecheră în buzunar!
Este uşor de închipuit cum am stat “ca pe ace” ca să se termine demonstraţia stupidă de la tablă şi cu aceasta şi ora, ca să fug la mama – pardon, la Tovarăşa Profesoară – să-i prezint isprava mea.
O singură întrebare mai rămâne de lămurit: de ce a ales mama cele trei probleme în această succesiune? Prima şi a treia au cam aceeaşi figură; a doua se integrează şi ea cumva. Nu ştiu ce să zic, dar momentul a fost superb.
Titus Grigorovici