PROPORŢIONALITATEA INVERSĂ
ŞI PARADIGMA SA
Cu multă vreme în urmă am primit un e-mail în care apărea următorul text, căruia nu-i cunosc provenienţa şi nici veridicitatea. Textul îmi pare însă realist, aşa că vi-l prezint în integralitatea sa:
MOTO: “E mult mai uşoară dezintegrarea unui atom decât a unei prejudecăţi”- Albert Einstein
CUM SE NAŞTE O PARADIGMĂ
Un grup de oameni de ştiinţă au pus într-o cuşcă cinci maimuţe şi în mijlocul cuştii o scară, iar deasupra scării o legătură de banane. Când o maimuţă se urca pe scară să ia banane, oamenii de ştiinţă aruncau câte o găleată cu apă rece pe celelalte, pe cele care rămâneau jos.
Dupa ceva timp, când o maimuţă încerca să urce scările, celelalte nu o lăsau să urce. După mai mult timp nici o maimuţă nu se mai suia pe scară, în ciuda tentaţiei bananelor.
Atunci, oamenii de ştiinţă au înlocuit o maimuţă. Primul lucru pe care l-a făcut aceasta a fost să se urce pe scară, dar a fost trasă înapoi de celelalte şi bătută. După câteva bătăi nici un membru al noului grup nu se mai urca pe scară.
A fost înlocuită o a doua maimuţă şi s-a întamplat acelaşi lucru. Prima maimuţă înlocuită a participat cu entuziasm la baterea novicelui.
Un al treilea individ a fost schimbat şi lucrurile s-au repetat. Al patrulea şi, în fine, al cincilea au fost schimbaţi.
În final, oamenii de ştiinţă au rămas cu cinci maimuţe care, deşi nu primiseră niciodata o baie cu apă rece, continuau să lovească maimuţele care încercau să ajungă la banane.
Dacă ar fi fost posibil ca maimuţele să fie întrebate de ce le băteau pe cele care încercau să se caţere pe scară, răspunsul ar fi fost: “Nu ştim. Lucrurile întotdeauna au fost aşa, aici… AŞA ESTE TRADIŢIA!”
Este ceea ce se întâmplă în fiecare ţară în care oamenii nu vor să ştie de ce unele lucruri sunt aşa cum sunt!
*
Să analizăm acum situaţia definirii proporţionalităţilor, care se dă de obicei în felul următor:
Definiţia 1: Numerele x, y, z se numesc direct proporţionale cu numerele a, b, c dacă avem 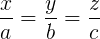 .
.
Definiţia 2: Numerele x, y, z se numesc invers proporţionale cu numerele a, b, c dacă avem 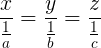 .
.
Nu ştiu de ce nu am şters textul de mai sus din calculator (cel cu maimuţele) atunci când l-am primit, dar de fiecare dată când văd prin cărţi sau la diferiţi colegi definiţia proporţionalitătii inverse, îmi aduc aminte de acest exemplu. După părerea mea, definiţia a doua ar trebui să sune astfel:
Definiţia 2 bis: Numerele x, y, z se numesc invers proporţionale cu numerele a, b, c dacă avem x ∙ a = y ∙ b = z ∙ c.
Oricine studiază fenomenul mai atent va vedea că această definiţie este corectă şi în plus este mult mai simplă. Atunci, de ce se dă elevilor complicaţiunea de mai sus? Fără să mai adaug şi situaţii stupide (destul de dese) când elevii primesc probleme de tipul: numerele x, y, z invers proporţionale cu numerele 1/2, 1/3, 1/5 etc.
În aceste cazuri ajungem la monstruozităţi de felul 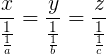 ,
,
în loc de mult mai blânda 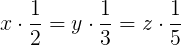 ,
,
care duce chiar la 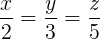 .
.
Deci, de ce se dă definiţia 2 elevilor? Eu văd doar o explicaţie. Este vorba de problemele de împărţire a unui număr în părţi proporţionale cu trei numere date. Aceste probleme, în cazul proporţionalităţii directe sunt destul de logice şi se rezolvau cu o teoremă bine cunoscută obţinută din lecţia despre proporţii derivate: 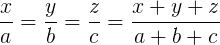 .
.
La proporţionalitatea indirectă însă, nu există o teoremă corespunzătoare, de exemplu ceva de felul: x ∙ a = y ∙ b = z ∙ c = (x + y + z) ∙ (a + b + c). Dar, nici un stress, problemiştii au forţat lucrurile şi au obţinut următoarea relaţie absolut corectă: 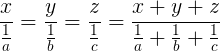 .
.
Atâta vreme cât se mai folosea această rezolvare, se justifica şi definiţia 2. Dar de câţiva ani colegii profesori au trecut cam toţi la o altă rezolvare pentru aceste probleme. Rezolvarea este asemănătoare la ambele tipuri de proporţionalitate şi se bazează pe folosirea lui k, foarte cunoscut de la raportul de asemănare. Din păcate însă, odată cu abandonarea rezolvărilor prin teorema arătată (atât în cazul PD cât şi în cazul PI), profesorii nu s-au gândit să abandoneze definiţia stupidă 2 şi să treacă la definiţia mult mai logică 2 bis. Dacă am întreba pe cineva de ce predă definiţia 2, s-ar putea să primim un răspuns de tipul “Nu ştim. Lucrurile întotdeauna au fost aşa, aici… AŞA ESTE TRADIŢIA!”. Îmi cer sincer scuze pentru comparaţie, dar tot asta îmi trece prin cap, de fiecare dată când văd undeva sau la cineva definiţia 2.
*
Haideţi să încheiem totuşi într-o notă mai optimistă. În primul rănd să concluzionăm. Eu le prezint elevilor următoarea variantă: la proporţionalitatea directă avem rapoarte egale, pe când la proporţionalitatea inversă avem produse egale.
M-am gândit foarte mult căutând un exemplu “practic” de împărţire a unui număr în părţi invers proporţionale cu mai multe numere şi iată ce am găsit:
Bunica aduce cadou o pungă cu 144 bombonele M&M celor trei nepoţi, cu cerinţa ca aceştia să le împartă între ei invers proporţional cu vârstele lor (logic, nu?). Stabiliţi câte bombonele primeşte fiecare nepot, ştiind că ei au vârstele de 18, 12 şi respectiv 9 ani. (cel de clasa a VI-a face rezolvarea, cel de liceu o verifică iar cel mic mănâncă cele mai multe bomboane)
Iată şi cum ar merge rezolvarea cu k. Notăm cu x, y, z numărul de bomboane primite de cei trei nepoţi, de vârste 18, 12 şi 9 ani. Proporţionalitatea inversă implică următorul şir de produse egale: 18 ∙ x = 12 ∙ y = 9 ∙ z ; să notăm aceste produse egale cu k, deci avem: 18 ∙ x = 12 ∙ y = 9 ∙ z = k. Din aceasta putem exprima fiecare cantitate necunoscută de bomboane în funcţie de k astfel: 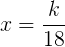 ,
, 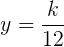 şi
şi 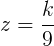 .
.
Dar, ştiind că x + y + z = 144, rezultă că 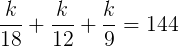 . După o scurtă muncă de rezolvare a acestei ecuaţii obţinem k = 576, iar apoi imediat: x = 32, y = 48 şi z = 64 bombonele (cel mic trebuie să primească cele mai multe bombonele, pe când cel mai mare, cele mai puţine; logic, nu?).
. După o scurtă muncă de rezolvare a acestei ecuaţii obţinem k = 576, iar apoi imediat: x = 32, y = 48 şi z = 64 bombonele (cel mic trebuie să primească cele mai multe bombonele, pe când cel mai mare, cele mai puţine; logic, nu?).
Titus Grigorovici



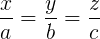 .
.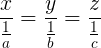 .
.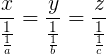 ,
,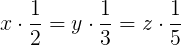 ,
,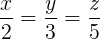 .
.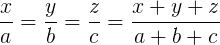 .
.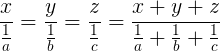 .
.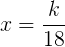 ,
, 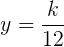 şi
şi 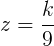 .
.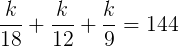 . După o scurtă muncă de rezolvare a acestei ecuaţii obţinem k = 576, iar apoi imediat: x = 32, y = 48 şi z = 64 bombonele (cel mic trebuie să primească cele mai multe bombonele, pe când cel mai mare, cele mai puţine; logic, nu?).
. După o scurtă muncă de rezolvare a acestei ecuaţii obţinem k = 576, iar apoi imediat: x = 32, y = 48 şi z = 64 bombonele (cel mic trebuie să primească cele mai multe bombonele, pe când cel mai mare, cele mai puţine; logic, nu?).
