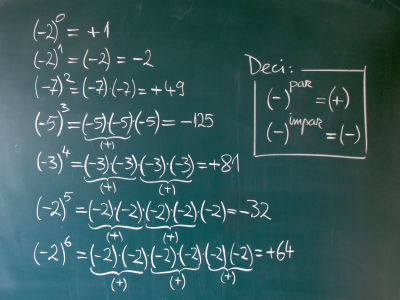De curând am prezentat cartea Marele roman al matematicii (Editura TREI, 2021), de Mickaël Launay. În următoarele rânduri doresc să vă prezint un citat din această carte, cât şi felul în care acesta mi-a influenţat o lecţie de clasa a 6-a, ajutându-mă să-mi îmbunătăţesc cu încă un pas arta predării matematicii (puteţi accesa prezentarea precedentă direct la adresa http://pentagonia.ro/prezentare-de-carte-marele-roman-al-matematicii-mickael-launay/). Iată pentru început pasajul respectiv (pag. 177-179), în descrierea autorului Mickaël Launay:
*
Unul dintre exemplele cele mai izbitoare mi s-a revelat într-o zi în care animam atelierul de cercetare împreună cu clasa a doua de la o şcoală (notă explicativă: în Franţa copiii merg la şcoală după împlinirea vârstei de 5 ani). Copiii, în jur de 7 ani, aveau ca sarcină să lucreze cu triunghiuri, pătrate, dreptunghiuri, pentagoane, hexagoane şi multe alte forme, pe care trebuiau să le trieze conform unor criterii liber alese. S-a observat că pentru fiecare dintre aceste figuri putem să numărăm câte laturi şi câte vârfuri există. Triunghiurile au 3 laturi şi 3 vârfuri, pătratele sau dreptunghiurile au 4 laturi şi 4 vârfuri şi aşa mai departe. Realizând această listă, copiii au formulat rapid o teoremă. Un poligon are întotdeauna tot atâtea laturi câte vârfuri.
Săptămâna următoare, pentru a-i provoca, am adus în discuţie figurile neregulate, dintre care una avea forma următoare: (aici este reprezentat în carte un patrulater concav)
Se pune, aşadar, întrebarea: câte laturi şi câte vârfuri există aici? Şi iată că majoritatea clasei răspunde: 4 laturi şi 3 vârfuri. Acest unghi inversat din josul figurii nu are o formă de vârf, adică nu este ascuţit (unghiul supraobtuz, adică cel având măsura mai mare de 180o). Nu se poate rostogoli figura peste el. Este mai degrabă o scobitură decât o umflătură a figurii. Pe scurt, acest unghi care intră în figură nu făcea parte din ideea prealabilă pe care copiii şi-o făcuseră despre ce este acela un vârf. Dacă le-aş fi cerut să numească acest punct “vârf”ar fi însemnat că le cer să dea acelaşi nume unor lucruri diferite. Ce idee stranie! Discuţiile s-au încins. Niciun copil nu este de acord cu statutul acestui nou punct. Ar trebui să-i dăm, oare, un alt nume, ar trebui să-l ignorăm complet? Există argumente pro şi contra, dar, în general, niciunul nu părea să convingă pe majoritatea dintre ei.
Apoi, dintr-odată, un copil şi-a adus aminte de teoremă. Dacă acesta nu este vârf, nu mai putem spune că orice poligon are tot atâtea laturi câte vârfuri. Spre marea mea uimire, acest argument a fost cel care într-o clipă a făcut ca întreaga clasă să-şi schimbe părerea. În câteva secunde toată lumea era de acord: trebuia ca acest punct să capete numele de vârf. Trebuia să fie salvată teorema, chiar cu preţul prejudecăţilor noastre. Ar fi fost păcat ca acest enunţ atât de simplu şi limpede să fi avut excepţii. Iată cea mai precoce manifestare a eleganţei matematicii la care am putut fi martor.
“Excepţiile” nu sunt frumoase. Ele ne rănesc sentimentele. Cu cât un enunţ este mai simplu şi aplicabilitatea sa mai mare, cu atât ne dă impresia că putem să atingem cu degetul ceva cu adevărat profund. Frumuseţea în matematică poate căpăta diverse forme, care se manifestă prin acest raport tulburător al complexităţii obiectelor studiate cu ajutorul formulărilor cât mai simple. O teorie frumoasă este o teorie economă, fără resturi, fără excepţii arbitrare şi deosebiri inutile. Este o teorie care spune multe cu puţine vorbe, care fixează esenţialul în câteva cuvinte, care merge direct la ţintă.
Dacă exemplul poligoanelor rămâne elementar, această impresie de eleganţă nu face nimic altceva decât să crească, pe măsură ce teoriile se dezvoltă, păstrând în acelaşi timp o ordine care se reduce la câteva reguli simple. (…) Este atât de frumoasă situaţia prezentată, atât de calde cuvintele la adresa matematicii, încât aici se simte pur şi simplu nevoia unei pauze scurte pentru savurarea acestui pasaj.
*
Despre această carte susţineam că ne poate influenţa pozitiv predarea, în sensul că ne-ar stimula înspre a le trezi elevilor bucuria de a face matematică. Spuneam că mi-o păstrez ca lectură de vacanţă, dar s-a apucat soţia să o citescă, iar când găsea ceva interesant îmi citea repede şi mie. Având în minte povestirea prezentată mai sus, peste două zile aceste idei m-au influenţat semnificativ în cadru unei lecţii, transformându-i finalul într-unul deosebit de captivant pentru elevi.
Clasa a 6-a s-a întors fizic în şcoală la Cluj spre finalul lunii Mai 2021. Aveam cam toate lecţiile importante parcurse, mai puţin cele despre introducerea noţiunii de numere pozitive respectiv negative. Lecţiile oficiale ne vorbesc despre Numere întregi, dar esenţa lucrurilor este despre apariţia în viaţa elevilor a numerelor negative, cât şi despre felul cum acestea se relaţionează cu cele vechi, care se numesc de acum încolo numere pozitive. M-am străduit să parcurg lecţiile la un nivel cât mai “basic” posibil, conştient fiind de faptul că elevii erau foarte bucuroşi de revenirea fizică în clasă, dar totodată aveau acumulată şi o cantitate uriaşă de frustrare generală împotriva matematicii, în urma celor cca. şase luni de izolare în online, de obicei singuri acasă, în care nu reuşiseră să se concentreze suficient pentru a primi mesajul matematic. Nu vroiam să le stric bucuria revenirii la şcoală cu o lecţie prea grea sau prea abstractă; de obicei mă străduiesc în acest sens, dar acum eram şi mai atent.
După lămurirea operaţiilor de ordinul I (adunarea şi scăderea) şi II (înmulţirea şi împărţirea), acum eram la ultima lecţie, cea despre puterea numerelor întregi (pentru pedanţi, mă refer desigur la puterea numerelor întregi negative cu exponent natural). Vroiam să o parcurg cu răbdare ca să o înţeleagă din prima cât mai mulţi elevi ai clasei, dar totodată doream să o termin repede (în cel mult 30 min.), pentru ca în ultimul sfert de oră să discutăm măcar puţin şi despre ordinea operaţiilor (mai aveam apoi încă o oră de geometrie şi o ultimă oră rezervată algebrei în care vroiam să dăm în sfârşit şi un mic test fizic în clasă; era în săptămâna dinainte de EN8, când urma să fim exilaţi din nou în online şi oricum trebuiau să fie încheiate mediile).
Trebuie desigur să precizez aici şi faptul că nici vorbă să mă gândesc să le turui lecţia; pentru mine nu intră în discuţie decât varianta de predare prin problematizare În pasajul următor vă prezint orientativ dialogul de “cucerire” a acestei lecţii cu elevii, pe care o putem denumi şi predare prin întrebări. Precizez că numerotarea întrebărilor este doar tehnică, folosită pentru claritatea acestui eseu; cu elevii, pe tablă nu le-am notat.
Întrebarea 1): Cât este (–5)3? Dezbatere, discuţii, păreri … . Până la urmă am ajuns la scrierea (–5)·(–5)·(–5). Primii doi de “minus” înmulţiţi dau “plus”, iar apoi, cu al treilea “minus” dă în total “minus”. Buuun! (trec peste “perlele” despre cât ar fi 53)
Întrebarea 2): Cât este (–3)4? Iarăşi puţină dezbatere, dar mult mai repede am ajuns din nou la scrierea (–3)·(–3)·(–3)·(–3). Aici elevii nici nu au imediat impulsul să grupeze primii doi de (–) într-un (+) şi, separat, ceilalţi doi de (–) într-un alt (+), ca apoi să concluzioneze că (+) ori (+) dă (+). NU, ei au impulsul să găsească semnul rezultatului altfel: primii doi de (–) cuplaţi dau un (+), apoi acesta împreună cu următorul (–) dau un (–), iar în final acesta cu ultimul (–) dă un (+); (apropos, şi la înmulţirea 3·3·3·3 gândesc la fel, adică 3·3 = 9, apoi 9·3 = 27, iar în final se blochează la 27·3; de fiecare dată trebuie să le tot repet că 3·3·3·3 = 9·9 care trimite mult mai uşor către 81). Oricum, până la urmă ajungem la acelaşi rezultat: (+). Interesaaant!
Întrebarea 3): Cât este (–2)5? Treaba merge deja mult mai rapid. Eu chiar îi temporizez pe cei care “s-au prins de mişcare” (încercând să am grijă astfel încât să-i duc pe cât mai mulţi elevi împreună cu noi în acest raţionament), aşa încât introduc din nou scrierea (–2)·(–2)·(–2)·(–2)·(–2), pe care putem însemna cu nişte acolade sub acest rând, îmbrăţişând tot câte două “minusuri” care dau un “plus”, în final rămânându-ne ultimul “minus”, care devine semnul rezultatului (aceleaşi acolade fuseseră folosite şi la primele două întrebări).
Întrebarea 4): Cât este (–2)6? Este evident că aici mulţi aveau răspunsul, dar pentru lămurirea definitivă a tuturor elevilor încă mai scriem (–2)·(–2)·(–2)·(–2)·(–2)·(–2). După reluarea acoladelor pentru a stabili semnul rezultatului, vine desigur şi întrebarea despre o regulă.
Întrebarea 5): Aşadar, care ar fi regula semnului la puterile cu baza negativă? Destul de repede elevii cei mai sprinţari spun că “minus la putere pară dă plus” şi “minus la putere impară dă minus” (aşa o spun ei, apoi eu le-o repet într-un limbaj mai tehnic, spunând-o încă o dată folosind cuvântul “exponent”).
Aceste puteri, corespunzând primelor cinci întrebări, le-am scris pe rânduri succesive, pornind “din mijloc”, adică lăsând câteva rânduri goale deasupra (elevii fuseseră avertizaţi să fie atenţi la dialogul de la tablă şi să nu scrie, pentru că eu voi scrie şi în jos şi în sus). După obţinerea acestei reguli, (pentru început exprimată doar oral) am continuat să scriu deasupra puterii a treia un nou rând cu puterea a doua: aşadar (–7)2 = (–7)·(–7). Acest rând apare doar ca o confirmare a teoriei proaspăt generate, în corelare cu mai vechea (–)·(–) = (+) Apoi am trecut la rândul gol de deasupra, cu următoarea situaţie.
Întrebarea 6): Cât este (–2)1? Din nou avem puţină dezbatere, dar repede ajungem la concluzia că (–2)1 = (–2) = –2. Aha, deci “minus doi” la puterea 1 dă semnul “minus” pentru că este o singură dată. Dar putem să zicem şi că avem “minus la o putere impară” care dă desigur “minus”. Această ultimă observaţie a fost făcută şi la puterea a doua, cele două împreună reconfirmând faptul că regula mai sus exprimată este corectă şi la puteri cu exponent mai mic (nu doar la puteri cu exponente tot mai mari). Acum vine ultima şi cea mai ciudată întrebare (scrisă din nou pe rândul liber de deasupra).
Întrebarea 7): Cât este (–2)0? Vă puteţi imagina desigur răspunsurile de tipul “minus zero!” sau “minus unu” (bazat pe amintirea că “ceva la puterea zero dă unu”). Aşadar cât dă? Desigur, cunoaştem din clasa a 5-a că “un număr la puterea zero dă unu”, dar asta era valabil la numerele naturale, adică pozitive, la “numerele fără minus”. Oare la numerele negative se păstrează regula că va da 1, sau aici va da –1? Că de zero ne-am lămurit repede că nu-i cazu’.
Aici s-a întâmplat ciudăţenia cu care nu ţin minte să mă mai fi confruntat în anii precedenţi: câţiva elevi nu erau în stare “să renunţe în sufletul lor” la acel “minus” de la bază. Baza acestei puteri are “minus”. Ei au înţeles că mai mulţi de “minus” dau “plus” (dacă se pot grupa câte două şi alte două etc.). Dar aici nu poate deveni “plus” pentru că nu avem “mai multe de minus”. Eu nu voiam să-mi argumentez răspunsul pe baza formulei din clasa a 5-a (şi eventual pe baza autorităţii mele), respectând faptul că într-adevăr, aici aveam nişte “numere noi” (este de bun simţ matematic că nu avem certitudinea păstrării regulii vechi la o situaţie nouă). Doi băieţi erau mai înverşunaţi în acest sens şi nu le venea a crede că acel “minus” dispare şi datorită faptului că în explicitarea lui (–2)0 de fapt nu mai avem nici un zero. Mulţi alţii erau derutaţi pentru că nu puteau citi pe faţa mea un verdict clar înspre varianta cu +1 (eu folosesc deseori în lecţie un fel de “poker-face” pentru a le forţa gândirea).
În acest moment eu am început să simt similitudinea deosebită cu povestea egalităţii numărului de laturi şi de colţuri din cartea lui Mickaël Launay, respectiv cu forţa “teoremei” găsite de către elevi. Aşa că le-am pus următoarea întrebare ajutătoare: păi. exponentul lui (–2)0 cum este, par sau impar? Brusc s-a făcut linişte în clasă, ochişorii de deasupra măştilor s-au mărit a uimire şi au apărut explicaţii de genul: zero este par, deci e clar că rezultatul este + 1, adică tot 1.
Bucuria s-a simţit prin toată clasa, mai ales la elevi pentru că, după suspansul creat, se găsise răspunsul fără echivoc. Dar bucuria era şi în sufletul meu, pentru că vedeam pe concret cum funcţionează mecanismul logic prezentat de Mickaël Launay, mecanism de trezire a bucuriei matematice în sufletul copiilor. Aşadar şi “teorema” din clasa a 5-a se păstrează, fiind salvată: orice număr la puterea zero ne dă tot unu, indiferent dacă numărul de la bază este pozitiv sau negativ. Imediat toţi au fost de acord cu acest răspuns şi nimeni nu mai vedea la (–2)0 un semn de minus la rezultat.
Legat de paritatea lui 0 (zero), trebuie precizat că acest aspect nu este evident pentru elevi. Doar întrebat direct, elevul, ajungând să se gândească, va decide că zero este par, iar asta mai mult pe baza faptului că stă vecin cu 1 (care este mai uşor de priceput că este impar) sau că este la două unităţi depărtare de numărul 2. Gândindu-se la această întrebare, de fapt nici cei mai mulţi adulţii nu realizează din start că zero este par (vorbesc aici de nematematicieni).
Iată, pentru claritatea eseului, poza de final a tablei, dar precizez încă o dată că eu le-am scris de la rândul din mijloc în jos, apoi de la rândul al treilea în sus, puterea cu exponentul 0 fiind ultima scrisă. În final am adăugat alături şi regula (“teorema”).
Evident că, după lămurirea lucrurilor şi ţinând cont că elevii au trebuit să fie atenţi şi să nu copieze de pe tablă (din cauză că eu scriam ba în jos ba în sus), elevii au primit câteva minute să-şi completeze în caiet întreaga schemă cu cele 7 rânduri de puteri (scrisă desigur de la puterea zero la puterea a 6-a), plus regulile aferente. Eu nu văd aceste minute ca o pierdere de timp, ci mai degrabă ca o scurtă şi rapidă recapitulare pentru fixarea noii situaţii, aşa încât momentul este profund benefic. Ca o ultimă idee, precizez că eu nu fac în clasă şi exemple cu puterea unui număr pozitiv. Consider că în urma unei înţelegeri bune a acestei lecţii, elevii trebuie să-şi dea singuri seama despre cum funcţionează puterea în cazul unei baze pozitive (apare la temă şi la test).
*
Putem în acest moment să ne aventurăm într-o scurtă analiză a fenomenului, astfel încât să înţelegem ce s-a întâmplat, să interiorizăm mecanismul psihologic ce are loc, ca apoi să fim în stare să folosim şi cu alte ocazii apariţia acestui fenomen în cadrul altor lecţii.
Eu puteam să le “turui” lecţia şi probabil o terminam mult mai repede. Puteam chiar să le dau eu noile reguli, eventual chiar sub forma clasicelor formule: (–1)2k = +1, respectiv (–1)2k+1 = –1, caz în care i-aş fi speriat pe cei mai mulţi dintre elevi (caz în care totodată şi pasam clar sarcina înţelegerii fenomenului acasă, la părinţi, eventual profesoriulor din particular). Mergând însă pe calea problematizării şi folosind o scriere cât mai accesibilă (şi un limbaj la fel de accesibil), în procesul de înţelegere a fenomenului şi de descoperire a “teoremei”, elevii s-au legat emoţional de aceasta, astfel încât în momentul când şi-au dat seama că “teorema lor” acţionează şi în noua, dar ciudata situaţie cu exponentul zero, în acest moment toată clasa a fost de acord că rezultatul este tot 1 (unu), această conştientizare fiind totodată însoţită şi de o mare satisfacţie.
O astfel de lecţie le aduce elevilor o stare de bucurie “liniştită”, o senzaţie că ei înţeleg lumea din jurul lor şi că “totul este în bună ordine”. Nu în ultimul rând, mintea lor a făcut un pas hotărâtor spre a-şi spori încrederea în gândirea matematică, controlând abstractizarea ei, pentru că acest pas a fost făcut pe baza înţelegerii şi a gândirii personale.
Eu nu le-am pus în faţă nişte rezultate neînţelese, ci i-am îndrumat pe o cale prin care ei să le descopere şi să înţeleagă fenomenul studiat. Faptul că ei au generat rezultatul le-a întărit şi mai mult încrederea şi convingerea în acest rezultat, în această “teoremă” descoperită chiar de către ei (la clasă nu i-am spus “teoremă”, dar folosesc aici acest cuvânt prin analogie cu “teorema” lui Mickaël Launay.
În cadrul lecţiei respective, ca o schelă de susţinere a gândirii, “teorema” lor le-a dat încrederea şi siguranţa în a face următorul pas, un pas ciudat, într-o zonă oarecum obscură şi greu de înţeles pentru mulţi elevi. Faptul că ei au descoperit-o le-a dat mult mai multă încredere în acest rezultat decât dacă le-aş fi dat eu “teorema”. Dacă le dădeam eu “teorema”, aceasta le-ar fi fost străină, dar aşa, descoperind-o ei, gândirea lor “o avea în suflet”, înţelegând deci imediat şi acceptând de la sine noul pas. Chiar dacă descoperirea a fost făcută sub îndrumarea întrebărilor mele (folosind predare prin întrebări), aceasta acţionează asupra elevilor care s-au implicat în mod emoţional: ei au găsit-o, au înţeles-o şi le este dragă, o respectă şi nu ar accepta un rezultat care să o contrazică.
Probabil că acest fenomen este unul dintre principalele cauze pentru care elevii din clasele mele povestesc acasă că le place la matematică, şi în general îi refuză pe părinţi atunci când aceştia se implică şi vor să le predea un anumit subiect înainte acasă. E clar că vorbesc aici de elevii care sunt dispuşi şi reuşesc să se implice regulat în procesul de generare a lecţiilor, atunci când fac predare prin problematizare. Aceştia nu mai au ulterior nevoie de a învăţa acasă lecţia cu pricina, pentru că au prins noile idei în mod sănătos din clasă.
Metoda funcţionează chiar şi la elevii mai timizi, cei care nu au curajul să se exprime oral, dar care în sinea lor urmăresc fiecare pas al lecţiei, au de obicei răspunsul “pe limbă” dar, timizi fiind, aşteaptă să-l dea altcineva. Eu îi văd clar şi pe aceştia, le văd “lumina din ochi” şi am astfel certitudinea că “sunt cu noi”, cu cei care purtăm dialogul de generare a lecţiei (ei cumva “stau în spatele” celor care participă cu curaj la datul benevol al răspunsurilor).
Chiar mai mult, şi ei la rândul lor se simt clar percepuţi, văzând cum îi urmăresc în scurtele momente de contact vizual. În timiditatea lor introvertită, acestora le este suficient şi le dă o siguranţă blândă. Asta se întâmplă atunci când suntem fizic în clasă. Din păcate în online mi-a fost mult mai greu să-i percep. În online, contactul vizual nu mai există. Mulţi dintre aceşti elevi simţindu-se în sufletul lor neglijaţi, de la o vreme au început să decadă.
Revenind la predarea fizic în clasă, desigur că cei care se mulţumesc doar la a copia de pe tablă, a căror implicare în ora de matematică se rezumă doar la copierea lecţiei, rămânând de multe ori şi în urmă, aceştia nu ajung să se lege emoţional de noile cunoştinţe. Pentru ei predarea prin problematizare nu are efectele scontate. Uneori îmi este ciudă pe aceştia şi pe indolenţa lor. Atunci îmi închipui cum părintele îi spune unui astfel de copil la plecarea de acasă să fie cuminte şi să scrie totul de pe tablă. Îmi închipui cum nu-i cere să fie atent sau să fie activ la ora de mate. Probabil că îi spune doar să scrie totul de pe tablă, aşa încât el/ea se rezumă la a scrie totul de pe tablă. Pentru aceşti elevi şi eleve este nevoie de alte abordări, dar despre ei voi discuta cu o altă ocazie (promit că în curând).
Încercând să finalizez, eu consider că în acest spectru ar trebui citit Marele roman al matematicii al lui Mickaël Launay, dar şi multe altele dintre cărţile despre bucuria palpitantă a matematicii. Găsiţi o listă orientativă a acestora în postarea http://pentagonia.ro/prezentare-de-carte-anii-de-aur-ai-cartilor-despre-matematica/ . Titus Grigorovici