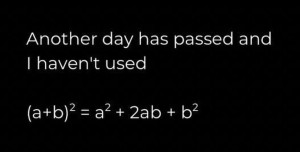Arta predării matematicii
Vorbeam înainte de Crăciun de multitudinea de brăduleţi matematici. În perioada ce a urmat au tot apărut alţi şi alţi brăduţi, unii mai frumoşi decât ceilalţi. Chiar dacă sezonul lor a trecut, ne permitem să vă prezentăm la superofertă încă cinci exemplare superbe. Moş Costică
Încă două exemple de la colega noastră mioritică:
Da, şi încă un exemplu mai geometric:
P.S. Da, şi mai avem şi o concluzie în urma acestei perioade de intense colinde:
Toate marile lanţuri de magazine oferă în vremea asta spre vânzare şi brazi de Crăciun. Peste tot e aceeaşi atmosferă de bucurie focusată pe brazi şi pe decoraţiuni. Sâmbătă seara, într-un magazin Dedeman, de-abia am putut ieşi cu căruciorul printre toţi cei mulţi din faţa magazinului, care-şi alegeau un brad sau aşteptau să le fie împachetat. Era o imagine minunată cu mulţi brazi şi cu vânzoleala oamenilor de tot felul. Am reuşit cu greu să trec, iar apoi în drumul meu către maşină am cules de jos câteva crenguţe căzute de la cei care cumpăraseră deja, iar acum se îndreptau mulţumiţi spre casă cu brăduţul ales. Vă invit şi pe dvs. la un mic târg al brăduţilor unui Crăciun matematic. Pe unii îi cunoaştem, pe alţii nu, dar avem cu toţii ocazia să petrecem puţin timp în jurul unei idei simpatice (dacă n-aţi făcut-o deja, poza circulând de o vreme pe net). Moş Costică
Ca matematician român, dar vorbitor fluent de limba germană (până în a 8-a la clasă de secţie maternă germană), creierul meu nu are probleme din a trece de la 92 din română (nouă zeci şi doi) la 92 din germană: zwei und neunzig (doi şi nouă zeci).
Ok, aici aveam în copilărie anumite probleme pentru că încurcam în germană numărul 19 cu numărul 90. Astfel, 19 se spune ad litteram “nouă zece”, pe când 90 se spune “nouă + zig” (ce-o fi însemnând acest “zig”, asta nu ştiu; poate o ştiu doar lingviştii nemţi). Mult mi-a trebuit până s-au fixat corect “pe creier” acestea. “Liniştea interioară” mi-am găsit-o doar după ce mi-am imaginat nişte oameni din vechime spunând 9 cu mâinile şi arătând apoi spre degetele de la picioare (încălţate sau nu, unde mai avem încă 10 degete). De fapt ceva similar avem şi noi în română: nouăsprezece (la nouă-spre-zece imaginaţi-vă arătând cu mâna în jos spre picioare când spun spre zece).
Apropos: nemţii denumesc degetele de la mână “Finger” (un cuvânt de sine stătător), pe când degetele de la picioare ca “Zehen” (pronunţat ţeăn), cuvânt care sugerează clar 10, semănând puternic cu “zecele” nemţesc: “Zen” (pronunţat “ţen”).
În aceste condiţii, ca om ce m-am chinuit toată viaţa să-mi lămuresc cât de cât franceza (fiind la mine doar a treia limbă străină, pe lângă româna maternă, germana de fapt străină, dar super intensă, şi engleza care “venea tare din urmă”), eram foarte mândru de cum se spun numerele în germană, comparat cu ciudăţenia din franceză: quatre-vingt-douze. Oricum, şi asta am mai înţeles-o, văzând în acest vingt (20) o reminiscenţă a unei baze de numeraţie absolut naturale pe baza faptului că “calculatorul nostru la purtător” are în set complet 20 de degete (zece la mâini şi zece la picioare, de obicei ascunse, adică încălţate). De unde vine acest vingt (20) din franceză, asta nu mi-am făcut gânduri până acum.
Mult mai greu mi-a fost însă să mă obişnuiesc cu spusul orelor în germană: momentul de la ora 4 şi jumătate (16;30) se spune în nemţeşte Halb Fünf, adică jumătate cinci. Foarte greu mi-a fost, a durat ani şi ani până am prins ideea şi încă câţiva până am ajuns să o pot folosi ca atare. Salvarea mi-a venit din raţiunea că intervalul de timp orar dintre ora patru fix şi ora cinci fix este de fapt ce-a de-a cincea oră (am trăit fenomenul la intrarea în anul 2000, când nematematicienii susţineau că se schimbă mileniul, pe când matematicienii râdeau, conştienţi fiind că mileniul urma să se schimbe la sfârşitul lui 2000, la trecerea în 2001). Astfel, prima oră începe de la miezul nopţii, sau de la miezul zilei, şi se termină complet atunci când ceasul “bate ora 1”. Ca urmare, eu m-am liniştit şi am putut folosi sistemul corect şi natural când mi-am tradus în minte Jumate cinci în Jumătatea celei de-a cincea ore; de fapt asta înseamnă ca moment în timp ora 4:30.
Da, acesta este “istoricul” meu. Apoi, prin vară (primăvară) a apărut de undeva următoarea imagine, cu o informaţie despre citirea numărului 92 la danezi: 2 + (5 – 0,5)·20.
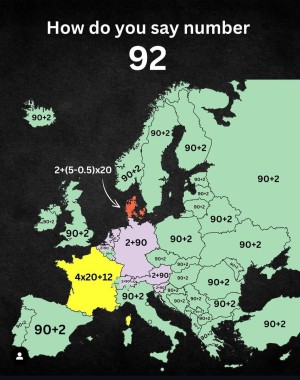
Ce-o fi asta? Iniţial mă gândeam să lansez aici o dezbatere, să ne spună şi nouă cineva care se pricepe, care-i faza cu această citire dubioasă (îmi cer scuze că nu vorbesc daneză; cel mai nordic punct al Europei unde am ajuns a fost Hamburg în Germania; mai departe doar “la televizor”). Apoi, din întâmplare, am dat pe Google.de dar scriind numerele pe germană (deci dând spre căutare: zwei und neunzig auf dänisch însemnând 92 pe daneză). Şi să vedeţi voi ce minunată discuţie am găsit pe Reddit. De fapt nu o redau aici complet pentru că este plină de comentarii şi divagaţii (dar totul în parametrii unei conversaţii civilizate, fără certuri şi înjosiri, ca la mioritici). Cred că mai bine încerc să vă prezint aici un fel de rezumat al celor găsite acolo. Tot ce scriu în continuare trebuie citit însă sub “rezerva” că sunt preluate din acele comentarii, deci nu au fost verificate din alte surse (dacă cineva se pricepe mai bine, este invitat să aducă lămuriri). Aşadar, iată un rezumat a celor spuse (în germană) de către nişte danezi:
Noi spunem: to og halvfems, care tradus cuvânt cu cuvânt înseamnă doi şi nouăzeci. Halvfems este pur şi simplu cuvântul pentru nouăzeci. Originea cuvântului provine însă de la un fel de numeraţie în baza 20, pe când rădăcina cuvântului din engleză ninety (9×10) provine din numeraţia în baza 10. Nu este însă aşa că noi încă mai socotim în acest fel. Este vorba doar despre un “cuvânt” care a fost scurtat cu timpul. Cuvântul complet ar fi fost halvfemsindstyvende, aşa cum în engleză denumirea completă ar fi fost nine tens (nouă zeci, doar că în română se scrie legat).
Apoi am luat din sistemul de numeraţie francez 20-ul, dar folosind ordinea numerelor germană (deci unităţile citite înaintea zecilor; eu mă gândesc aici că poate francezii au luat 20-ul de la vikingi, în urma aşezării acestora în Normandia).
Apoi am mai adăugat Slang şi am abandonat 20-ul, pentru că deveniseră numerele prea lungi. Da, avem unul dintre cele mai nebune şi incestuase sisteme numerice din lume.
Între timp, la suedezi se spune direct în baza zece: 53 înseamnă pe suedeză femtiotre, care înseamnă exact cincizeci şi trei.
Este aşa cum este, însă doar emigranţii mai fac greşeli. Copiii se obişnuiesc din prima şi nu greşesc defel la învăţarea şi la folosirea numerelor.
Este vorba de un proces istoric, cum am ajuns aici, dar nimeni nu se mai gândeşte la vechile forme de exprimare a numerelor. Acum sunt doar numere pentru 20 sau 90. Acestea provin dintr-un sistem profund logic, care folosea modalităţi de a spune numerele care azi ne apar neobişnuite, dar care în urmă cu sute de ani erau răspândite în Europa. Se pot observa rămăşiţe ale sistemului de numeraţie cu 20 (în baza 20?) în multe locuri, la fel cum se pot observa elemente ale sistemului Jumătate-N în felul în care noi (şi alţi scandinavi) exprimăm timpul ( ei spun că “zic timpul”, nu ca noi românii, care întrebăm “cât e ora”). Jumătate-patru înseamnă ora 3:30 (la scandinavi, dar, cum am mai spus, şi la nemţi). Nu e nimic “nebun” la asta, doar neobişnuit pentru voi.
Este forma veche de a spune numerele; acum folosim o formă “mai puţin ciudată”. Analizată însă, aceasta arată astfel: pe sistem vechi aveam bis og halv fem sinds tyve, adică 2 şi ½5 de 20 de ori. Acum am lăsat deoparte tyve, ceea ce face numărul mai ciudat, dar mai scurt. În plus s-a modificat pronunţia, aşa încât nu se mai aude ca ½5, ci ca ceva de sine stătător, astfel încât totalul înseamnă simplu 90. Deci şi noi spunem de fapt 2 şi 90.
Pe engleză mai sunt oameni care-şi aduc aminte că “12 şi 4 Score ani” însemna 92 de ani. Score reprezenta 20. Acest “Score” vine din vechea limbă nordică (a vikingilor) şi se referea la un băţ pe care se însemna numărul animalelor (probabil reni, dar şi alte bovine) prin crestături. Bănuiesc că un “Stock” (tradus aici “băţ”, preluat din germană, unde se pronunţă “Ştoc”) însemna cândva un “20” de animale (putem în paralel să ne întrebăm cum a evoluat cuvântul englezesc respectiv spre “score” de la fotbal, care la noi a evoluat în scorul unui meci).
Cei mai mulţi danezi oricum nu cunosc etimologia: “jumătatea celui de-al cincelea punct” (deci 4 ½ sau 4,50). Ei învaţă doar pe de rost că acesta este numele acelui număr. Părerea mea este că e într-adevăr ciudat că nu desfiinţăm asta şi să preluăm sistemul cu zeci, dar realitatea e că unii ţin la acest sistem.
Da, iar acum alegeţi-vă singuri de pe net un salut de final în daneză (eventual întrebându-l pe AI). CTG
P.S. Şi alte ţări au ciudăţenii numerice. Puteţi lua ca temă de studiu, de pildă, în câte forme apare numărul zero la englezi, în funcţie de context.
În ultima vreme au apărut două zile speciale, având fiecare însemnătate numerică aparte. În primul rând am avut ziua de 16 septembrie 2025, care a fost prezentată ca ziua mondială Pitagora, în sensul că putea fi spusă ca 16.9.25, implicând astfel pătratele numerelor care compun ca laturi triunghiul dreptunghic cu laturile (3;4;5), cunoscut şi ca “triunghi egiptean” (era folosit în Egiptul antic, mult înaintea lui Pitagora, pentru trasarea unghiurilor drepte pe teren, atât în măsurarea parcelelor după inundaţiile anuale ale Nilului, cât şi în alte proiecte de construcţii). Ca o observaţie scurtă, în sistemul american de scriere, această dată apare ca 9.16.25 (perfect corespunzătoare scrierii triunghiului cu laturile în ordine crescătoare). În mod oarecum similar am fi putut sărbătorii şi alte date, de pildă 5 dec. 2013 (5.12.13), sau la anu’ 24 oct. 2026 (10.24.26) etc.
În altă ordine de idei, de curând am avut o aşa-numită zi pătrată globală, care s-a petrecut în 27 septembrie 2025, pe baza faptului că 27.09.2025 luat ca număr de opt cifre este un număr pătrat: 27052025 = 52052. Interesant este că la fel avem şi în cazul scrierii americane a datei, adică 9.27.2025, la care avem că 9272025 = 30452.
Nu ştiu cum e la alţii, dar eu m-am întâlnit în ultima vreme destul de des cu această întrebare, legată de diferiţi itemi de învăţat în orele de matematică (bănuiesc că sunt mai des întâlnite în gimnaziu). În acest context a mai apărut încă o astfel observaţie, prezentată sub formă de glumă: o altă zi trecută în care n-am fost nevoit să folosesc (a + b)2 = a2 + 2ab + b2. E clar că gluma este valabilă doar pentru “oameni normali”, nu şi pentru practicanţi “obişnuiţi” de matematică şcolară (de pildă, în vederea examenelor). CTG
Dacă tot ne-am plimbat prin Sicilia, în ton cu sezonul, vara aste ne-am putut răcori şi cu un Peroni nastro azurro. Aşa cum ne spune şi reclama respectivă care nu ratează nici măcar o pauză publicitară: Lasă-te inspirat de noile Peroni limoni di Sicilia şi Peroni arancia rossa cu 0.0% alcool!
Cum??? N-aţi înţeles? Păi, fiind citită, la televizor reclama este mult mai clară:
Cu zero punct zero la sută alcool!
Da’ de când nu se mai spune zero virgulă zero? Serios?! Sau, eventual, cum spun alţi producători, cu zero la sută alcool.
Dacă aţi ratat cumva reclama, o găsiţi la https://www.youtube.com/watch?v=s2Zn_cjw1Rw
Lăsând gluma de-o parte, tot mai des auzim minunăţia asta cu punct în loc de virgulă la fracţii zecimale, citire ce este preluată din cultura americană (şi din limbajele gândite de ei pentru calculatoare). O fi bine, o fi rău? Oricum, când un copil îmi spune cu punct în loc de virgulă, eu deduc că acesta stă cam mult pe calculator sau telefon, pe filmuleţe care scriu fracţile zecimale “în americăneşte”.
O fi şi o umbră de analfabetism funcţional numeric aici? Păi, eu când trec dintr-o limbă în cealaltă, spun numerele ca în limba respectivă: 2 şi 90 dacă trebuie să spun 92 pe germană, sau 9.2 în loc de 9,2 dacă trebuie să vorbesc pe engleză (mai greu îmi este pe franceză cu numerele până la 100). Chiar aşa, da-n italiană cum se scriu fracţile zecimale? Cu virgulă sau cu punct? Titus Nonalcoholicus
Când mi-a spus o elevă dragă că merge scurt în Italia cu familia, între publicarea rezultatelor la EN şi perioada de admitere la liceu, am întrebat doar dacă merg cu maşina sau zboară, gândindu-mă deci că “merg în Italia”. Şi brusc, într-o zi, am primit următoarea poză:
Uitându-mă mai exact “am ridicat sprâncenele” şi am cerut lămuriri. Dialogul de la distanţă a fost scurt: –Voi v-aţi dus în Siracuza? -Da, noi am mers pentru peisaje, ulterior am aflat că acolo a trăit Arhimede. Imaginea este cu vitrina unui magazin din Ortigia, lângă Siracuza în Sicilia.
O concluzie colaterală mi-a fulgerat prin cap: pierdute în eterul visării fură poveştile mele despre Arhimede, din timpul orelor de geometrie, chiar şi cele din destul de recenta oră despre sferă, cu Romanii care vroiau să cucerească Sicilia la Siracuza, cu Arhimede acolo … E clar că sunt “bune” poveştile în ora de matematică, mai trece vremea! Dar să nu ne amăgim că le vor şi ţine minte elevii. Şi totuşi, parcă ceva tot a rămas acolo, în memorie, la 10 zile după examen, un pic de conexiune cu vechile poveşti, dar şi faptul că Arhimede a arătat că aria sferei este de 4 ori cât aria cercului de aceeaşi rază (cum mi-a spus la întoarcere).
Dacă nu v-aţi uitat cu atenţie, la exponatele din vitrină, faceţi-o măcar acum: poza este plină de π-uri în toate formele. La întoarcere am primit ca souvenir şi un breloc cu π:
Pentru cei care doriţi detalii (poate vă gândiţi să comandaţi), anexez şi poza cu spatele cutiuţei în care era ambalat brelocul respectiv (firma pare că se numeşte ARCHITOYS; îmi cer scuze că nu mă mai obosesc să ofer şi o traducere).
Pe lângă denumirea de “constanta lui Arhimede”, pe mine mă distrează cel mai mult afirmaţia cum că Arhimede a fost primul care l-a calculat pe π cu două zecimale exacte. Analizând obiectiv lucrurile, trebuie să recunoaştem că acesta este nivelul de matematică ce trebuie ştiut de omul de rând. Realitatea, pe care ar trebui noi să o prezentăm elevilor (chiar dacă o vor uita imediat), realitatea istorică a fost însă puţin diferită: Arhimede a calculat acest raport ca 22/7 (am putea scrie şi 22:7). Numerele zecimale, cele cu virgulă, au fost inventate olecuţă mai târziu, dar da, împărţind 22 la 7 obţinem exactitate până la nivelul sutimilor.
Iar cu asta ajungem, ca noutate, la o a doua, respectiv o nouă posibilă ziua lui π. Aşadar, La mulţi ani! de ziua aproximării lui π care ar fi deci evident pe 22 iulie (22.7 – Happy pi approximation day!). CTG&ZaraHola
Suntem obişnuiţi să aflăm din “perlele” candidaţilor la examenele de limba şi literatura română, presa centrală de Bucureşti oferindu-ne de obicei o scurtă selecţie în acest sens. Perle din zona matematică nu prea ajung publice, greşelile de gândire sau de calcul fiind foarte greu vizibile la nivelul corectării lucrărilor, dar şi destul de seci în sensul “gustării” de către publicul larg (după principiul că “nu toată lumea e obligată să ştie matematică” sau “poţi trăi bine şi fără matematică”).
Anul acesta am avut norocul de un elev foarte cinstit, care mi-a prezentat plin de entuziasm rezolvarea sa de la exerxiţiul 5 din Sub. I, de la simularea naţională a EN. Iată pe scurt rezolvarea exerciţiului, aşa cum mi-a fost prezentată cu mare avânt de către respectivul elev (cu mare avânt, pentru că ştia deja că a ales răspunsul corect):
Nu aţi înţeles? Nici eu n-am înţeles din prima, aşa că l-am oprit şi am cerut explicaţii mai lente, pas cu pas, ca să înţeleg şi eu ceva. Iată şi pentru dvs. paşii separaţi, din care puteţi deduce greşeleile individuale. Astfel, îmi spuse elevul următoarele:
– La început am zis că e supra 2, că-s două numere a şi b; dar apoi am văzut că de fapt sunt patru numere, aşa că am scris supra 4.
– Astea două se duc (minus radical din 2 cu plus radical din 2).
– La fel şi astea două (4 – 4 = 0).
– Deci rezultatul este 4.
Ultima concluzie este o cumulare a mai multor greşeli, pe care merită să le analizăm separat. În primul rând, mulţi elevi “începători în ale matematicii” nu înţeleg diferenţa între simplificare, unde ‘nimic” înseamnă 1, şi respectiv reducerea termenilor opuşi într-o sumă, unde “nimic” înseamnă 0; la ambele avem situaţia cu o tăiere lângă care nu mai scriem nimic. Această greşeală s-a combinat aici cu o a doua: nimic (interpretat ca 1) supra 4 a fost încurcat în mintiuca acestui elev cu 4 supra 1. Elevul respectiv ţinea minte că una din acestea dă 4, numărul 1 dispărând. Aşa că a bifat rezultatul 4, care era printre variantele posibile. Super! Eu personal nu am mai văzut o astfel de combinaţie de 5 greşeli în cascadă, care să ducă la rezultatul corect (desigur, cu sprijinul total dezinteresat al sistemului de testare în grilă).
Mie îmi place să colecţionez. Orice tip de item frumos ce îmi apare în 2-3 exemplare care se potrivesc împreună poate reprezenta baza unei noi colecţi. N-am ce face: sunt profund atras de frumos în toate formele posibile. Fie că sunt cutii de cafea din tablă sau pahare de vin de un anumit fel, nimic nu-mi scapă impulsului nestăvilit de colecţionar de frumos. Şi nici problemele de matematică frumoase nu fac excepţie de la acest impuls. În acest sens se încadrează şi micro-colecţia de faţă.
Problema centrală, în jurul căreia este construită această colecţie, o aveam de mult timp, de prin 2005, din perioada când am strâns probleme pentru culegerea publicată la editura Humanitas Educaţional, iar în toţi aceşti ani am tot apelat la aceasta ca un foarte bun exemplu de aplicaţie al teoremei “ciocului de cioară”. Dar aceasta se şi poate aplica – ca atare sau doar ca idee de lucru – şi în alte probleme ale acestui grup, astfel încât am cadorisit-o pentru moment cu titlul de “teoremă” pentru unele din probleme ce i s-au alăturat în colecţie.
Colecţia însă s-a declanşat vara 2023, cu “o ridicare de sprânceană”, la apariţia problemei cu cercul de arie π din triunghiul egiptean cu laturile de (3, 4, 5), care este cu adevărat o problemă uimitoare (putem spune liniştiţi că reprezintă “problema vedetă” a setului). Aceasta se poate numi o problemă frumoasă. Odată declanşat interesul, setul de faţă a fost colecţionat în anul şcolar următor, toate problemele fiind preluate de pe grupuri de facebook din străinătate (orientativ din Asia de sud), arătând o ciudată efervescenţă, gen brain storming între profesori de la distanţă, între diferite persoane active pe acele grupuri în acea perioadă, a căror imaginaţie se activa la vederea problemelor precedente (sau, pe care poate le aveau dinainte).
Eu nu ştiu pentru ce clase au fost gândite aceste probleme de către profesorii respectivi “de peste mări şi ţări”, dar putem desigur să ne gândim unde ne-ar fi bune nouă. Ţinând cont că în unele rezolvări sunt necesare formulele de calcul prescurtat (pătratul sumei, la nivel elementar), dar şi rezolvarea ecuaţiei de gradul II, eu consider că în semestrul 2 din clasa a 8-a ar fi momentul cel mai bun de abordare a acestei fişe ca întreg (ar fi păcat să le despărţim, deşi s-ar putea şi aşa, ţinând cont că baza geometrică este cunoscută din clasa a 7-a). Astfel, putem prezenta acest set elevilor de a 8-a sub titlu recapitulativ (eu exact aşa l-am şi gândit: pentru elevii dragi din cele două clase de-a 8-a din acest an, ca un cadou matematic de activare a conexiunilor de gândire între diverşii itemi învăţaţi în clasa a 7-a şi a 8-a*).
Cele şase probleme colecţionate gravitează – la propriu şi la figurat – în jurul “teoremei” centrale, folosind elemente din aceasta sau din demonstraţia acesteia, aidoma unui grup de şase balerine în jurul prim-balerinei într-un moment de balet al gândirii geometrice împletită cu cea algebrică. Atenţionez că figurile sunt doar orientative, fiind construite “după ochi”, doar cu o monedă de 50 de bani şi o riglă negradată. Precizez încă o dată că aceste probleme nu sunt creaţia mea, doar colecţia fiind meritul meu (şi al soţiei). Totodată atrag atenţia că am încercat pe cât posibil să păstrez stilul de prezentare din postările originale, adică probleme cu un text minim, uneori doar cu date şi semne de întrebare pe figură, forţând astfel activarea gândirii rezolvitorului (cui nu-i convine acest stil, asta e!). Desigur că s-ar putea gândi şi alte variaţiuni şi “complicaţiuni” pe această linie, dar eu am încercat să mă rezum la colecţia respectivă, aşa cum a venit această către noi dinspre Oceanul Indian, inclusiv în sensul că acestea erau postate fără unităţi de măsură (puteţi ataşa cm sau cm2 pe fişa ataşată şi în pdf în final).
PS: *Cele două clase a 8-a la care predau au muncit în această perioadă la un proiect, fiecare elev redactând în orice formă o prezentare a unei pasiuni personale (unii au făcut-o în scris, alţii au făcut un panou de poze, alţii au adus o prezentare în PowerPoint, făcând-o singuri sau poate ajutaţi de acasă, fiecare după puterile sale). Din respect pentru colega ce a condus această acţiune, dar şi pentru elevii care au pus suflet în acest proiect, le dedic această micro-colecţie, ce poate fi privită şi sub titlul de participare din partea mea alături de ei la proiect: da, colecţionarea unor seturi de probleme pe o anumită temă reprezintă clar o pasiune de-a mea. Şi ce ocazie mai bună puteam să găsesc pentru prezentarea acestei colecţie decât ziua lui π! Cu şi pentru elevii respectivi am făcut anul trecut lipirea lui π pe treptele şcolii, iar anul acesta vom parcurge această fişă. Titus Grigorovici
PPS: Săptămâna asta, pe 10 martie s-au împlinit 5 ani de când am fost trimişi acasă “probabil pentru două săptămâni” din cauza Covid 19. Restul “poveştii” îl cunoaşteţi fiecare. Soţia mea evoca deseori titlul lui Jules Verne “Doi ani de vacanţă”. Mie îmi tot venea în minte refrenul de la REM: “It’s the end of the world, as we know it, and I feel fine.” Acum, discutăm din când în când, atunci când vedem la diferite clase urmările acelor ani. De pildă, cei din clasa a 10-a stau prost cu proporţiile, pentru că în anul acela de online 2020-2021 erau în clasa a 6-a. Cine zice că s-a putut învăţa eficient, acela … Eu studiez actualmente pe cei din clasa a 5-a, pe care pandemia i-a prins în clasa pregătitoare, cu scris-cititul încă neînvăţat, la fel şi cu socotitul. Depinde ce-au reuşit să facă părinţii pe acasă, sub îndrumarea învăţătoarei. Ar merita să discutăm cândva mai în amănunt aceste aspecte.
După cum am văzut, numărulul acestui an ne oferă multe surprize aritmetico-algebrice. Cei pasionaţi de ciudate “potriveli” istorico-numerice desigur că “vor ridica o sprânceană” la următoarea potriveală: 1 + 3 + 5 + … + 89 = 2025.
Adică, pornind de la momentul ruperii oficiale de dictatura lui Ceauşescu, din finalul lui 1989, ce trimitere ciudată face această sumă având rezultatul 2025? Ce vrea să prezică?
Oricum – revenind cu picioarele pe pământ – această potriveală reprezintă o ocazie minunată să-i mai uluim un pic pe cei din jurul nostru, pe cei mai puţin dotaţi matematic desigur. Cât despre elevi, acest exemplu reprezintă o bună ocazie de a le mai oferi la oră o uimire cu ceva gen “magie matematică” (mă refer aici la elevii cam de la orice clasă începând din a 5-a, efectul de uimire fiind similar la orice vârstă, depinzând de fapt doar de nivelul de profunzime al gândirii matematice dezvoltate).