Geometria are două componente clar diferenţiate. Pe de o parte sunt elementele de măsurare şi calcul al diferitelor mărimi (de obicei lungimi şi determinarea unor perimetre, arii sau volume, dar uneori sunt implicate aici şi determinări de unghiuri). Calculele de perimetre şi arii ale figurilor plane sunt reunite în general sub denumirea de planimetrie, pe când calculele de arii şi volume ale corpurilor poartă denumirea generică de steriometrie. Pe de cealaltă parte sunt elementele de studiere a proprietăţilor diferitelor situaţii (figuri sau corpuri), proprietăţi ce trebuie dovedite prin demonstraţii. Celor două componente să le spunem pe scurt calcule geometrice şi demonstraţii geometrice. Aceste două vaste domenii de activitate a geometriei sunt destul de bine delimitate, deşi ele interferează în multe zone intens.
În prezentul eseu doresc să evidenţiez un anumit fenomen la care m-am referit de curând în “strigătul de indignare” http://pentagonia.ro/reforma-de-avarie-1/ despre “Reforma de avarie” declanşată în minister la sfârşitul lunii octombrie, când a devenit evident magnitudinea celui de-al doilea val al pandemiei. M-am mai referit la acest subiect şi într-un “strigăt de indignare” mai vechi, prin finalul lunii iunie 2020, în postarea de la adresa http://pentagonia.ro/en-2020-in-forma-de-avarie-si-excluderea-geometriei-aritmetice/ . Fenomenul despre care doresc să scriu a ajunns în cea mai dură actualitate pentru cei care “au ochi să să vadă”, dar pentru foarte mulţi acesta este încă invizibil. Din păcate însă, atunci când fenomenul va fi vizibil pentru toată lumea, va fi mult prea târziu, aşa cum se întâmplă de obicei în cazul majorităţii greşelilor educaţionale. De pildă, îmi şi imaginez cum “se vor cânta” toţi prin mass-media la următoarele teste PISA.
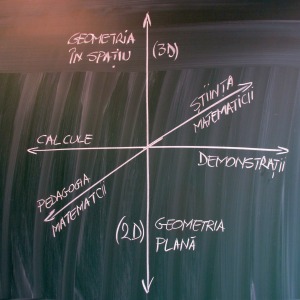
Pentru înţelegerea acestui fenomen este important ca cititorul să înţeleagă un câmp mai larg de aspecte ce influenţează predarea geometriei (pentru o lămurire cât mai bună rog cititorul să lectureze cu răbdare următoarele rânduri, acordându-mi creditul necesar, chiar dacă va părea o “teoria chibritului”, un “bla-bla”, un “bătut câmpii” fără un sens imediat)). Acest fenomen, despre care doresc să vorbesc, se află la concurenţa a trei axe de preocupare, ce trebuie lămurite în prealabil. Prima axă de preocupare este cea evidenţiată mai sus, anume axa de preocupare având într-o parte demonstraţia geometrică iar în cealaltă parte calculul diferitelor mărimi.
În studiul nostru, o a doua axă de discuţii o reprezintă parcurgerea materiei de la geometria plană la geometria în spaţiu (de la 2D la 3D, dacă este să folosim limbajul cu care sunt obişnuiţi mulţi copii), ordine faţă de care nimeni nu are obiecţii: de când lumea şi pământul studiul geometriei a plecat de la geometria plană spre geometria în spaţiu, deşi dacă ne gândim puţin, vom conştientiza că oamenii s-au confruntat de la începuturi în egală măsură cu geometria plană cât şi cu cea în spaţiu. Totuşi, dacă ne-am propune să analizăm ceva mai profund, eu cred chiar că în realitate oamenii au început să conştientizeze geometria prin construcţii, adică în 3D, dar au realizat imediat că aceasta se bazează pe proprietăţi ale geometriei plane, pe care au studiat-o mai clar, fiind mai accesibilă.
Există însă şi un exemplu unde din motive practice cunoaşterea a avut loc sigur datorită unor situaţii în 2D: mă refer aici la nevoia de măsurare a terenurilor – de unde vine chiar denumirea geometriei – şi vorbesc aici despre situaţia cu care se confruntau oamenii în Egiptul antic, chiar de la începuturile culturii apărută în valea Nilului, înconjurată de deşert, anume de necesitatea trasării urgente a parcelelor ţăranilor pe terenurile de pe care tocmai se retrăseseră apele Nilului după inundaţiile anuale. Acel teren mocirlos trebuia repede şi eficient delimitat celor ce urmau să-l lucreze pentru ca aceştia să-l poată însămânţa şi să pornească germinaţia. De la acest process au preluat grecii denumirea de geo-metria.
O a treia axă de interes pentru subiectul nostru o reprezintă axa ce uneşte cele două extreme preocupaţinale ale matematicii: predarea matematicii în şcoli şi matematica ca ştiinţă riguroasă (chiar prima ştiinţă ce s-a confruntat cu necesitatea unei rigurozităţi extreme). Este “la mintea cocoşului” că ordinea în care aceste două domenii pot apărea în viaţa unui om este cea prezentată aici: întâi îi este predată matematica elevului şi doar ulterior acesta, fostul elev, poate eventual ajunge ca matematician să practice ştiinţa matematică. Doar că “Nea Euclid”, în strădania sa de a organiza cât mai bine predarea, le-a cam amestecat cele două părţi. Restul “amestecăturii” şi inversarea ordinii naturale a acestor două etape l-au făcut ulterior urmaşii lui Euclid, acest proces de inversare a ordinii ajungând în secolul XX la un nivel obsesiv.
Astfel, pe de o parte avem impulsul natural din punct de vedere ştiinţific, anume strădania de ordonare teoretică riguroasă, pornind de la axiome şi construind pe baza definiţiilor şi a teoremelor toată geometria; acest sistem este cunoscut pe scurt ca sistem axiomatic sau euclidian, după numele celui care l-a introdus prima dată. Cel puţin în ultimele câteva secole toţi matematicienii s-au străduit să-l imite şi să-i perfecţioneze sistemul.
Pe de cealaltă parte avem necesitatea pedagogică naturală de a prezenta elevilor cunoştinţele într-o formă pe care aceştia să o şi înţeleagă, să le fie adusă în mod accesibil minţii lor de începători în ale geometriei. Aici există o sumedenie de reţete şi principii de abordare ce ne pot ghida în acest proces şi pot fi susţinute inclusiv din punct de vedere al psihologiei. Enumăr doar câteva: în primul rând ar fi predarea intuitivă, apoi predarea de la întreg la componente, la fel aş putea aminti predarea de la superficial la studiul profund, ce poate fi aplicată uneori în forma de predare în spirală, iar exemplele pot continua mult şi bine. În eseul de faţă mă voi referi la toate acestea atunci când voi vorbi de folosirea intuiţiei în predare, ca reprezentant al tuturor acestor mecanisme corecte din punct de vedere psihologic în procesul de cunoaştere a lumii.
Eu consider că marea dramă a predării matematicii în general, respectiv a geometriei în particular, o reprezintă obsesia matematicienilor din ultimul secol înspre direcţia unei ordonări axiomatic-ştiinţifice, dar din păcate automat în detrimental nevoilor psihologice ale elevului începător în studiul acestei materii (am scris foarte mult în ultimii cinci ani despre acest subiect, a fost una dintre preocupările mele de bază).
Concret, eu consider că intrarea în lumea geometriei se poate face doar prin zona intuitivă cu conexiuni practice, forma perfect ordonată din punct de vedere euclidian fiind potrivită doar ultimului nivel de cunoaştere a geometriei, anume cel ştiinţific. Predarea în şcoli a geometriei la nivelul primei treceri, adică la clasele gimnaziale, trebuie să respecte în primul rând principiile psihologice, cum ar fi intuiţia, şi doar dacă acestea sunt îndeplinite, putem să ne gândim ca predarea să capete şi anumite accente de ordonare euclidiană. O predare, adică o introducere a geometriei având în primul rând şi în mod obsesiv preocuparea de ordonare axiomatic-euclidiană (obsesie ce le-a fost impusă profesorilor din şcoli prin reforma uitată din 1980), o astfel de predare şi-ar avea loc doar la facultăţile de matematică, ca un exerciţiu de ordonare a introducerii cunoştinţelor; cel mult o astfel de formă de predare s-ar putea face eventual în clasele de liceu, însă la acest nivel doar cu anumite concesii în direcţia unei ordonări obsedate a rigurozităţii (ceea ce s-a şi întâmplat în manualele din 1978, dar aceste gânduri oricum nu mai sunt de actualitate din 1997 încoace, de când oricum nu se mai predă geometria sintetică în liceu).
Să rezumăm: pentru a înţelege fenomenul studiat, am propus un context format din trei axe de preocupare: 1) axa calcule – demonstraţii; 2) axa 2D – 3D; 3) axa pedagogie – ştiinţă. Ordinea dintre predarea cunoştinţelor legate de calcule şi a celor legate de demonstraţii poate fi analizată realist doar ţinând cont şi de celelalte două axe de discuţie. Altfel spus, ordinea justă a aranjării în materia şcolară a calculelor şi a demonstraţilor geometrice se poate face doar în contextul înţelegerii depline a celorlalte două direcţii preocupaţionale ale geometriei. În următoarele părţi ale acestui eseu voi face des trimiteri la argumente legate de confluenţa acestor trei axe. Constantin Titus Grigorovici