La peste un sfert de secol după schimbările din 1990 în şcolile din România se folosesc încă instrumentele de tip vechi. Nu vreau să susţin că acestea sunt depăşite; şi eu le cer elevilor în clasa a VI-a cunoscutele truse chinezeşti în cutiuţă de metal care îi ajută să înţeleagă toate mişcările specifice. Din clasa a VII-a le cer însă achiziţionarea unui alt instrument. Despre ce este vorba?
În vestul Europei se foloseşte de mult timp un instrument din plastic transparent care poate face orice construcţie în afara de trasarea cercurilor. Acesta este cunoscut sub denumirea de echer geometric: Geo-dreieck în germană pe scurt (complet ar fi Geometrie-Dreieck), Equerre géometrique pe franceză, Geometrical square pe engleză, Escuadra geometrica pe spaniolă, Triangolo Geometrico pe italiană etc. Iată o imagine cu acesta:
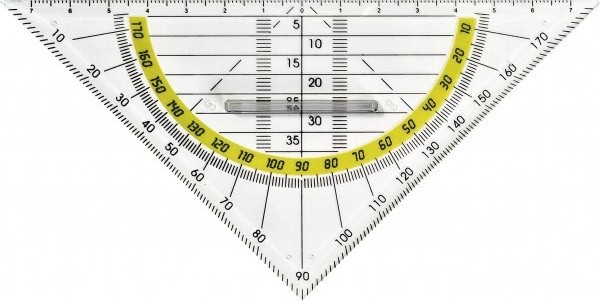
Haideţi să-l analizăm pas cu pas în elementele sale. În primul rând ne uităm la sistemul de linii paralele (paralele cu ipotenuza echerului), din 5 în 5 mm depărtate de ipotenuză. Cu acestea poţi trasa paralele la o dreaptă. Dacă punctul prin care doreşti să trasezi paralela nu este la distanţă de 5, 10, 15 etc. cm, atunci te poţi ajuta de cele două gradaţii suplimentare în mm cu care poţi poziţiona ipotenuza paralel faţă de dreapta iniţială.
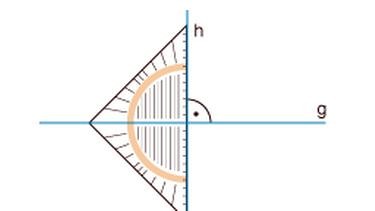
Al doilea element important este linia mediană a acestui echer (îmi place să numesc astfel înălţimea din unghiul drept pe ipotenuza echerului, totodată şi mediană, bisectoare, mediatoare şi axă de simetrie a instrumentului). Cu ajutorul acesteia în primul rând se pot trasa perpendiculare pe o dreaptă dată, perpendiculare care să traverseze dreapta. O astfel de perpendiculară este mult mai bună pentru că poate trece dintr-o parte în cealaltă a dreptei iniţiale “dintr-o mişcare”, fără mutarea echerului şi fără acea “rotunjire” deranjantă la piciorul perpendicularei, ce apare “vrei-nu vrei” la echerele de modă veche (dacă vrei perpendiculară doar pe o parte, te opreşti la dreaptă). Este atât de comodă trasarea perpendicularelor cu această linie mediană, încât cine s-a obişnuit să o folosească nu va mai accepta să lucreze cu alte echere.
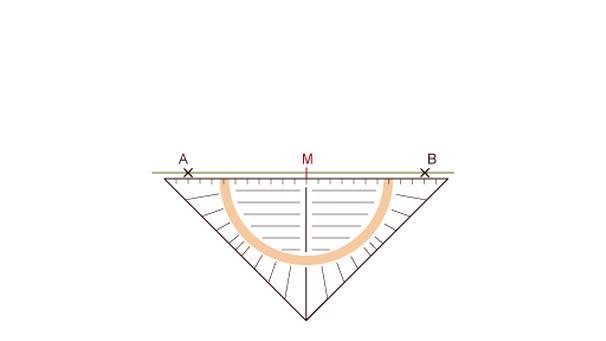
Probabil că aşteptaţi să vorbesc şi de raportor, elementul cel mai vizibil, dar nu, al treilea element valoros la echerul geometric îl reprezintă gradaţia liniarului de pe ipotenuză, avându-l pe zero la mijloc, numerele crescând în ambele părţi. Cu ajutorul acesteia se poate în primul rând găsi mijlocul unui segment, fără a-l măsura şi a împărţi lungimea la doi. Pur şi simplu trebuie să poziţionezi liniarul gradat de pe ipotenuză pe segment cu capetele acestuia egal depărtate de mijlocul zero, punct pe care îl însemnăm ca mijloc.
Combinând linia mediană cu gradaţia liniarului putem foarte uşor să construim bisectoarea unui unghi. Pentru asta trebuie să poziţionăm echerul geometric cu linia mediană trecând prin vârful unghiului şi laturile unghiului tăind gradaţia liniarului de pe ipotenuză în două puncte simetrice faţă de zero, în mod similar cum am procedat la mijlocul unui segment. Practic, astfel aranjate laturile unghiului şi cu liniarul gradat în cm cuprind între ele un triunghi isoscel, linia mediană a echerului ca înălţime devenind automat şi bisectoare.
Vine în sfârşit şi raportorul la rând de a fi analizat. Acesta nu aduce numic nou faţă de ce ştie toată lumea, dar trebuie folosit cu atenţie pentru că baza sa este chiar ipotenuza echerului şi nu o linie trasată pe suprafaţa interioară a plasticul echerului (vedeţi că pe echer nu sunt scrise valorile de 0o respectiv 180o, linia unghiului alungit 0o-0-180o fiind chiar liniarul gradat în cm al echerului, punctul 0 fiind vârful acestui unghi alungit). În mod similar cu construcţia unghiurilor drepte, aceste echere geometrice au şi nişte linii ajutătoare pentru construcţia unui unghi de 45o. În plus, având suprapunerea dintre centrul raportorului şi originea gradaţiei de pe liniar se pot trasa foarte uşor segmente de o anumită lungime la o anumită înclinaţie faţă de un segment dat (tocmai am descris construcţia triunghiurilor în cazul LUL).
Folosind linia mediană şi gradaţia ciudată a liniarului, putem construi foarte uşor şi simetricul unui punct sau al unei întregi figuri faţă de o dreaptă (privită ca axă de simetrie). Ştiu că astfel de sarcini nu sunt în repertoriul orelor de geometrie din România, dar am ţinut să prezint şi acest aspect deosebit de folositor în practică.
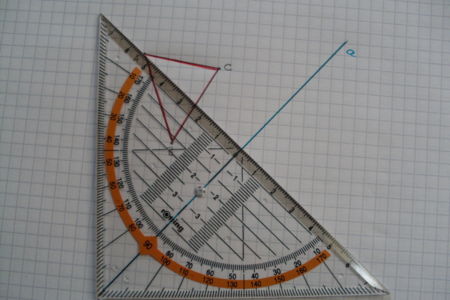
Vedeţi deci cât este de folositor acest instrument, permiţând construcţii foarte exacte atât pe foaia de matematică cu pătrăţele, dar în poziţii înclinate, cât şi pe coală velină (folosită la examenul de la finalul clasei a VIII-a sau la BAC). Să vedeţi ce uşor desenezi cu echerul geometric clasica figură din teorema lui Pitagora (cea cu pătratele construite pe fiecare latură a triunghiului dreptunghic)! Dar să luăm şi un exemplu mai simplu: construiţi cu echerul geometric un triunghi dreptunghic cu ipotenuza orizontală şi unghiul drept în vârf. La fel de folositor este echerul geometric şi la trasarea sistemului de axe ortogonale cu unităţi pe cele două axe ale sale, pentru trasarea punctelor şi a graficelor funcţiilor (desigur, pe foaie velină, când nu ai reperele pre-trasate ale pătrăţelelor de pe foaia caietului tradiţional de matematică). Da, echerul geometric construieşte aproape orice; doar cercuri nu ştie trasa.
Unde se găsesc astfel de instrumente valoroase? Am mai spus, sincere mulţumiri magazinelor Lidl care au tăria de a aduce măcar în fiecare septembrie astfel de echere în truse deosebit de ieftine (un echer geometric mic, unul mare şi un liniar ordinar) la 4 lei. Şi alte magazine aduc, dar neconstant şi de obicei la preţuri mult mai piperate, şi asta doar pentru că nu există o cerere constantă şi în cantităţi mari. De ce nu există această cerere? Pentru că şi după un sfert de secol de la “eliberarea oficială de comunism” organizatorii programelor şi a manualelor de matematică româneşti nu au preluat acest echer, ne-existând o recomandare oficială pentru folosirea sa.
În acest sens am o scurtă, dar edificatoare povestioară: prin 1992 m-am adresat conducerii întreprinderii Napochim din Cluj, care pe lângă lighiane şi alte castroane, producea şi instrumente geometrice din plastic transparent, cerându-le să introducă în producţie şi astfel de echere. Mi-au răspuns sec că, fie rezolv ca înainte să fie introduse prin materia din manuale, fie să plătesc eu realizarea matriţei. Am întrebat cât costă matriţa şi răspunsul “m-a dat pe spate”: era vorba de salariul meu de începător pe mai mult de un an. Q.E.D. La castroane şi lighiane aveau garanţia că se vând, la aceste instrumente deştepte aveau mari dubii. Şi uite-aşa au dispărut încet toate capacităţile de producţie româneşti, refuzând progresul.
Desigur că există echere geometrice şi mari, pentru uzul profesorilor la tablă (tot din import, e clar). Nu sunt ieftine, dar merită şi profesorul un instrument bun (iar şcolile la ora actuală chiar îşi pot permite astfel de achiziţii).
Închei această prezentare cu o precizare: imaginile de mai sus sunt toate culese de pe internet. Dacă daţi cuvinte de căutare denumirea echerului geometric în diferite limbi străine vă vor apărea şi filmuleţe postate în care puteţi vedea cum se foloseşte acesta. Dau un singur exemplu, anume un filmuleţ cu paşii de urmat pentru trasarea mediatoarei (în germană Mittelsenkrechte).
Mittelsenkrechte und Winkelhalbierende
Este interesant că autorul trasează mediatoarea cu echerul geometric, dar la bisectoare (în germană Winkelhalbierende) foloseşte metoda antică cu compasul, dovedind astfel o ciudată inconsecvenţă. Eu personal îi învăţ pe elevi în clasa a VI-a metodele tradiţionale cu rigla negradată şi compasul, iar din clasa a VII-a metodele mai moderne şi mai rapide cu echerul geometric.
Căutaţi şi cumpăraţi un astfel de echer, folosiţi-l şi veţi vedea că merită. Noi îl folosim de prin ’93-’94 şi elevii noştri a avut de atunci întotdeauna cele mai frumoase desene la examene. Titus G.
