De curând am aflat veşti îmbucurătoare din partea CEAE – Centrul de evaluare şi analize educaţionale, despre proiectul Matematica Altfel, ce susţine predarea prin investigaţie, o strategie inductivă de “cucerire” a matematicii de către elevi, printr-un proces de “cercetare”, însoţiţi cu tact de către profesori.
Cândva, în perioada în care citeam prezentarea de pe site-ul CEAE şi redactam selecţia din materialul pentru primul episod din această serie, cam în acele zile am avut la clasă o lecţie ce părea a se potrivi perfect cu tema, aşa încât am decis să o ofer ca un posibil exemplu (deşi, concret, nici nu ştiu cum arată tehnicile prezentate în cursurile CEAE). Aşadar, doresc să vă prezint cum predau eu de 25 de ani lecţia despre ariile figurilor de bază în toamna clasei a 7-a, printr-un proces de însoţire a gândirii elevilor înspre descoperirea respectivelor reguli (organizare gândită spontan la clasa a 7-a de atunci, exact cu 25 de ani în urmă; desigur că lecţia a fost supusă unui proces natural de cizelare în toţi aceşti ani, cu variaţiuni de la o clasă la alta, dar forma a rămas în mare parte, la fel).
Veţi putea vedea cum încerc eu să-i îndrum pe elevi pe un drum de matematică-proces, într-o stare de explorare, înspre descoperirea formulelor specifice. Eu fac aceasta pe baza unor figuri tip, la care adăugăm însă – din mers – diferite construcţii ajutătoare care sugerează şi explică apariţia formulei. Apoi, veţi vedea cum pornim a doua zi de lucru mai întâi cu cristalizarea acestora în matematica-rezultat, prin reluarea formulelor lângă figuri curate (adică lângă figuri tip, fără desenele ajutătoare din ora trecută, din timpul procesului de explorare). Cu alte cuvinte, veţi putea vedea cum elevii iau contact mai întâi cu matematica-proces, reprezentând gândirea şi înţelegerea fenomenelor respective, pe când în ora următoare apare matematica-rezultat, aducând perechile figură + formulă aşa cum trebuie acestea de fapt învăţate pe de rost pentru aplicarea în probleme.
În conexiune cu finalul episodului precedent al acestei serii, trebuie să precizez că este mult mai bine să lăsăm partea de cristalizare pentru ora următoare, chiar dacă aceasta este extrem de simplă. La fel ca şi în cazul unui film bun, dorim a-i lăsa pe elevi în atmosfera repectivă de cercetare, unde concentrarea era asupra diferitelor “mişcări” cu suprafeţe pe bază de triunghiuri congruente (completate de mişcările diferite de la trapez). Preocuparea din această lecţie a reprezentat-o găsirea reţetelor, nu aplicarea lor în probleme. Cu alte cuvinte, preocuparea acestei lecţii a reprezentat-o matematica-proces. Apoi, de-abia în ora următoare, apare matematica-rezultat, al cărei obiectiv principal îl reprezintă aplicarea în probleme (!!!).
Merită să precizăm aici şi un aspect ceva mai filozofic. Matematica-rezultat şi însuşirea acesteia se verifică – prin aplicarea în probleme – la teste, apoi desigur şi la examen. De aia toată lumea se concentrează asupra ei. Dimpotrivă, matematica-proces nu este verificată nicăieri (din câte am auzit era verificată pe vremuri, până prin anii ’70, când la Bacalaureat elevii trebuiau să susţină şi un examen oral). Din acest motiv nimeni nu-i dă atenţie. Doar că numai matematica-proces este formatoare de gândire matematică adevărată şi aducătoare de înţelegere a fenomenului studiat. Matematica-rezultat aduce doar “înţelegerea” paşilor din aplicarea în probleme (care este un alt tip de înţelegere şi de gândire, o inteligenţă “executorie”). Matematica-proces face conexiuni mult mai puternice între emisferele cerebrale, decât simpla învăţare şi aplicare a matematicii-rezultat. Matematica-proces produce pe durată oameni care gândesc cu adevărat, pe când matematica-rezultat produce doar buni aplicatori ai unor procedee gândite de alţii (!!!).
Găsim aici iarăşi o explicaţie a fenomenului de manipulare masivă a electoratului român la alegerile cvasi-eşuate din 2024-2025: românii sunt antrenaţi în şcoală înspre a fi buni executanţi ai unor procedee gândite de altcineva, dar pe care nu le şi înţeleg. Pur şi simplu, matematica din şcoala românească nu-i obişnuieşte pe elevi să participe la gândirea lecţiei, ci doar să execute şi să o aplice fără să comenteze. Cu alte cuvinte, nu-i obişnuieşte să gândească şi să se implice în organizarea unui proces ce urmează a fi creat, ci îi obişnuieşte doar să aplice un proces gândit de către alţcineva. Dar, să revenim la subiectul nostru.
Înainte de a începe prezentarea şi pozele tablei doresc să fac câteva precizări pregătitoare. În primul rând trebuie înţeles că forma de predare la care am ajuns reprezintă o formă de mijloc între predarea prin prelegere (care este destul de eficientă temporal, mergând cât de repede consideră profesorul pe moment) şi predarea prin descoperire, prin problematizare, până la urmă prin investigare şi explorare, prin care elevii descoperă de fapt informaţiile noi.
Concret, în desfăşurarea lecţiei caut o formă de echilibru între conducerea lecţiei de către profesor şi implicarea activă a elevilor. Astfel, lecţia se desfăşoară cu mine scriind la tablă şi cu elevii în bănci scriind în caietele lor. În acest fel eu dau forma ordonată a ceea ce ajunge în lecţie, ei copiază cât pot de bine, imitând cât mai ordonat cele de pe tablă (fiecare după posibilităţi). Dar, la fiecare pas ce trebuie făcut, eu expun situaţia, “problema” pe care o avem de rezolvat, sarcina pe care trebuie să o descoperim, la care elevii doritori din clasă se implică cu răspunsuri (cu cei nedoritori, …). Eu nu merg mai departe, preferabil, decât dacă am primit răspunsuri viabile, pe baza cărora să putem scrie ceva corect.
Desigur că acest sistem de predare funcţionează natural doar dacă elevii participanţi nu au învăţat deja informaţiile respective înainte, de acasă sau de la orele private. Când avem astfel de situaţii, convenţia este ca cel în cauză să nu se implice cu ceea ce deja ştie, perturbând astfel procesul de “cercetare”, el rămânând să privească acest dialog doar ca un spectator.
Un alt aspect îl reprezintă faptul că eu încerc să păstrez cât mai mult din lecţie prezentă pe tablă, aşa încât nu risipesc defel spaţiu (tabla fiind uneori cam înghesuită). Elevii sunt obişnuiţi ca la ei în caiete să nu se înghesuie aşa de tare, dar să păstreze ordinea. Clasa la care am predat acum această lecţie are o tablă de 4m, aşa încât în orice moment putem privi înapoi la momente similare sau la situaţii conectate de momentul în care suntem. Pentru articolul de faţă am tăiat însă pozele tablei în bucăţi mai uşor de privit pe ecrane.
Înainte de a începe trebuie să vă prezint şi structura lecţiilor pe care le aveam deja parcurse şi de care ne-am putut folosi în această lecţie, atât în partea teoretică, cât şi apoi în partea de aplicaţii imediate. Astfel, elevii cunoşteau deja rădăcina pătrată şi diferite metode de extragere a radicalului în cazul numerelor pătrate. Apoi, cunoşteau din clasa a 6-a şi foloseam deja de câteva ore intens teorema lui Pitagora pe diferite figuri pentru calcularea perimetrelor. Acum, pe lângă stabilizarea simţului pentru arie (unii elevii mai încurcă aria cu perimetrul), preocuparea principală consta în găsirea formulelor de arie pentru cât mai multe figuri deja cunoscute şi stabilizarea folosirii lor concrete (la nivel aritmetic, de calcul). Desigur că erau cunoscute şi toate felurile de triunghiuri, dar şi toate patrulaterele din programă. Materialul ce urmează prezintă preocuparea de bază despre calculul ariilor, material pe care îl consider obligatoriu pentru toţi copiii, în vederea promovării clasei. În această parte nu am abordat defel alte proprietăţi ale ariei (cum ar fi de pildă proprietatea de arie a medianei). Materialul de faţă prezintă doar preocuparea pentru calculul de arii şi perimetre.
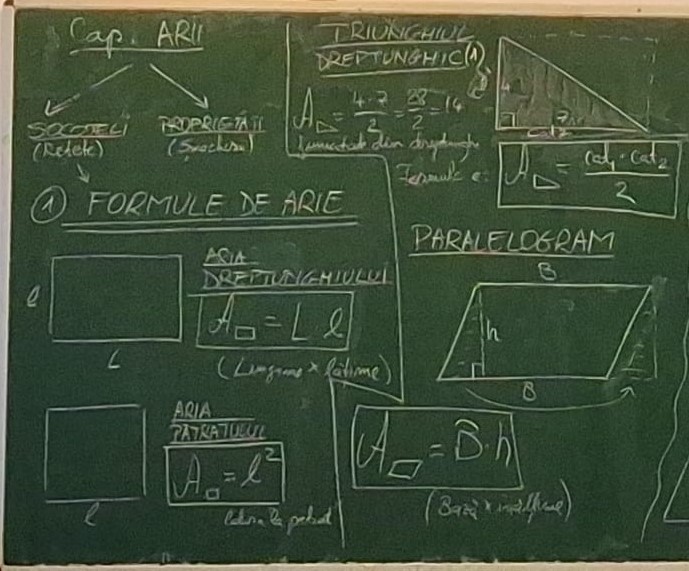
Procesul de lucru a început de fapt în ora precedentă (cca. 20min.) printr-o recapitulare a cunoştinţelor despre arie din clasa a 5-a, insistând pe explicarea logicii celor două formule: principiul de arie a dreptunghiului (un hol cu 4 rânduri de plăci de gresie, fiecare a 7 plăci, adică 7×4, deci lungimea ori lăţimea), apoi a faptului că la pătrat putem aplica formula de la dreptunghi, dar şi că la pătrat apare de fapt fenomenul “numerelor pătrate” (că de aia se numesc aşa) cunoscute tot din clasa a 5-a.
În plus, am discutat apoi următoarea întrebare: pentru situaţia când lungimea şi lăţimea unui dreptunghi sunt numere întregi, fenomenul este logic iar generalizarea rezultatului la formulă clară. Ce se întâmplă însă dacă lungimea şi/sau lăţimea nu sunt numere naturale? Exemplul de studiu din poza a doua îmi aparţine şi ţin foarte mult la el, mai ales că rezultatul întreg al ariei poate fi prezentat şi grafic (elevii trebuind să-l facă exact pe baza pătrăţelelor din caiet).
Ziua următoare am recapitulat pe scurt formulele celor două figuri iniţiale, după care am început căutarea formulelor pentru noi figuri. În acest sens trebuie să precizez că această lecţie a durat cca 70min. pe parcursul a două ore legate. Totodată, aşa cum veţi putea observa, cucerirea noilor formule are loc într-o ordine naturală pentru gândire, nu într-o ordine obişnuită a ordonării materiei (adică nu la început triunghiuri, iar apoi patrulatere), s-au într-o ordine obişnuită a teoriei matematice (adică nu mai întâi formula generală pentru triunghiul oarecare şi doar apoi cazurile sale particulare).
Cu alte cuvinte, prin selectarea ordinii de descoperit, am ales cea mai naturală cale pentru paşii de făcut de către mintea şi gândirea copilului într-un proces de descoperire a materiei. Precizez încă o dată: eu decid care figură urmează şi tot eu fac destul de repede şi o figură corespunzătoare pe tablă, însoţită de întrebarea “jucăuşă”: oare cum ar trebui să facem aici?
Dacă elevii văd ideea şi răspund, chiar şi numai orientativ, atunci discutăm ce şi cum, facem eventualele adăugări la desenul iniţial, deducem reţeta oral (de obicei un elev mai rapid de minte), iar apoi scriem reţeta sub formă de formulă lângă figură (şi desigur toată lumea copiază în caiet). Dacă, în urma mai multor încercări, nu vede nimeni ce-i de făcut, atunci ori mai insist cu informaţii ajutătoare ori, dacă “nu şi nu”, atunci ofer eu răspunsul (dar asta se întâmplă foarte rar şi doar când eu, ca dascăl, sunt constrâns de timp).
Aceasta ar fi forma ideală. Totuşi, de multe ori (depinzând de clasă) trebuie să dau eu primele idei, pentru că elevii pur şi simplu nu înţeleg ce ar trebui să facă. Anul acesta am avut totuşi bucuria să “curgă” cu idei folositoare de la primul pas; în schimb nu au prea avut idei de găsire a ariei trapezului, în finalul orei. Iată deci lecţia cu pricina (sper să vă descurcaţi în ordinea cam înghesuită de pe tablă), cu poza tăiată în trei părţi. Deci, după o nouă scurtă recapitulare a celor două iniţiale, la începutul orei (pentru elevii “din eşalonul de la coadă” nu sunt niciodată suficiente recapitulări), am pornit cu figurile noi.
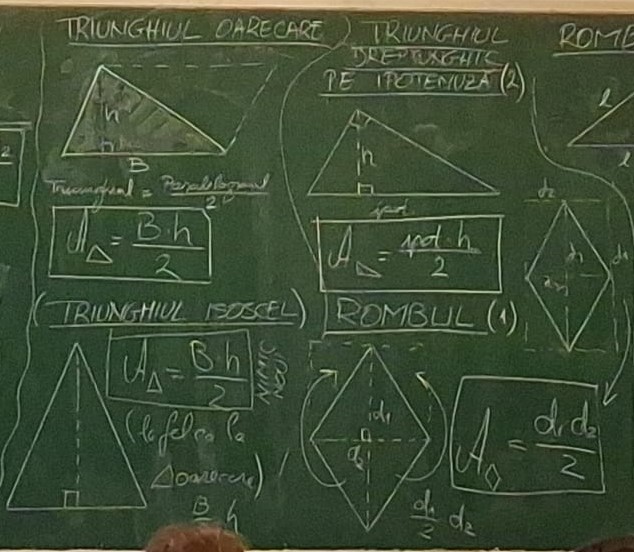
Aşadar, după părerea mea, cea mai uşor de dedus este aria triunghiului dreptunghic, ca jumătate dintr-un dreptunghi. Apoi urmează paralelogramul, căruia îi decupăm un triunghi determinat de înălţime, şi doar apoi triunghiul oarecare, ca jumătate dintr-un paralelogram.
De-a lungul anilor m-am tot întâlnit cu elevi nedumeriţi că nu găseau formula de arie a triunghiului isoscel, aşa că de o vreme o includ şi pe aceasta (cu parantezele şi explicaţiile de rigoare). Apoi apare, din acelaşi spectru, al nevoii elevilor ce gândesc mai puţin, şi aria triunghiului dreptunghic care “stă pe ipotenuză” (deci cu ipotenuza ca bază). Lecţia continuă cu aria rombului, aşezat în poziţia tradiţională, pe care eu o numesc “poziţia balerină”, deci cu o diagonală verticală şi una orizontală. La această figură am avut deja mai multe propuneri, iar eu doar le dădeam cuvântul elevilor, ca să avem o oarecare ordine (şi ca să nu se certe). Varianta posibilă cu rombul înscris într-un dreptunghi nu a văzut-o nimeni, aşa încât le-am spus-o eu în final, fără ca să o şi schiţez pe figură.
Însemnarea formulei respective cu (1) a fost făcută în momentul când i-am anunţat că la romb mai avem şi o a doua formulă, anume atunci când rombul stă “culcat pe o parte”, adică în “poziţia paralelogram”, scriind în acest timp şi titlul cu rombul (2). Aici au fost puţin surprinşi, dar repede careva din clasă a văzut conexiunea cu aria paralelogramului.
În acelaşi stil am dat apoi şi o a doua formulă pentru pătrat, atunci când pătratul stă în “poziţia romb”, după care am căutat şi formula. În această ordonare, finalul îi aparţine trapezului, la care eu mă opresc şi îi poftesc pe elevi să caute singuri o cale de a găsi formula. Cele mai vizuale sunt cuprinse în primele două figuri. Mai întâi dublarea trapezului pentru compunerea unui paralelogram de arie dublă, pe urma căreia găsim formula. Apoi apare şi varianta transformării trapezului într-un dreptunghi echivalent prin decuparea a două triunghiuri şi alipirea lor deasupra. Anul acesta nu a văzut nimeni aceste variante de lucru, iar când le-am arătat eu au fost foarte surprinşi. În alţi ani le vedea careva şi pe acestea (dar şi altele). În schimb, în acest an un elev a tăiat trapezul pe o diagonală, dar mai departe nu prea ştia clar ce să facă (voia să adune ariile celor două triunghiuri, dar încă nu avea forţa să scrie aria triunghiului care stă cu vârful în jos, în plus fiind şi obtuzunghic). Aşa că am preluat eu ideea şi i-am făcut o demonstraţie din aceasta, o demonstraţie mai algebrică.
Da, cam aşa arată lecţia, la care din păcate nu-i puteţi asculta şi sonorul cu dialogurile, uneori entuziasmante, din timpul descoperirii formulelor. În ora următoare am început din nou cu o recapitulare, de data aceasta formulele fiind organizate pe categorii, dar în primul rând fiind reluate fără completările de ora trecută pe baza cărora s-au dedus formulele. Acum apare doar figura tip curată şi formula (n-am scris nici măcar denumirea, ci doar le-am spus-o oral).
După această recapitulare (figurile rămânând deci pe tablă, gata de folosit), am pornit cu problemele. Eu continui această lecţie cu aplicaţii în calcul de arii şi perimetre la figurile studiate, întotdeauna conţinând desigur şi determinări de lungimi prin teorema lui Pitagora.
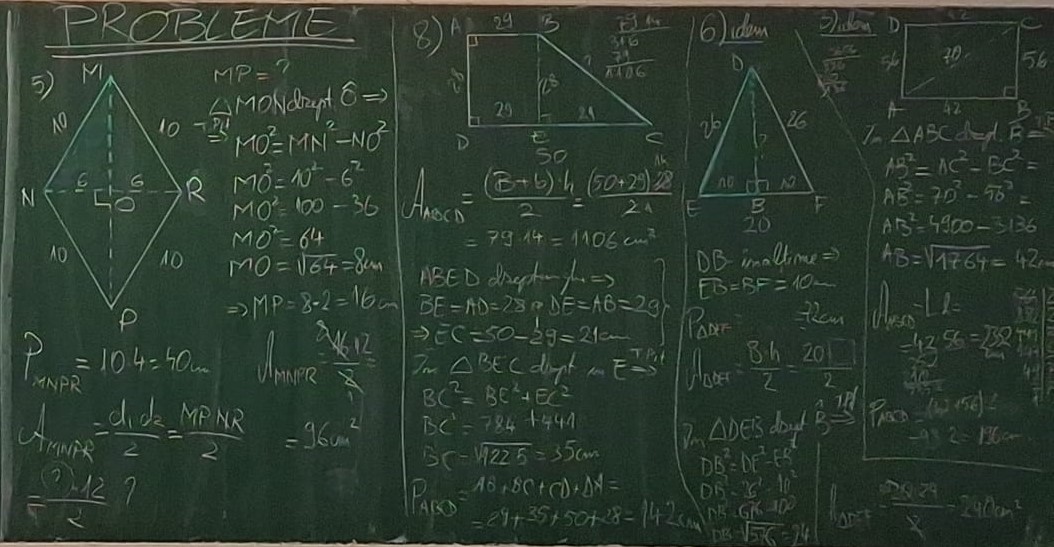
Este important ca în această oră să apară suficiente exemple cu diferite figuri, astfel încât elevii să priceapă cum se integrează de la sine teorema lui Pitagora în acestea, prezentă atât în formă de adunare (calcul de ipotenuză), cât şi în formă de scădere (calcul de catetă), învăţând să localizeze în aceste figuri triunghiuri dreptunghice pentru calculul necesar. În ora următoare am continuat cu probleme similare în alte figuri, elevii putând astfel observa cum se păstrează reţeta de lucru din ora precedentă, adaptată însă la acestea.

Puteţi observa desigur cum am venit cu situaţii tot mai alambicate (pentru elevul de rând), dar rămânând totuşi în spectrul numerelor naturale, adică a tripletelor pitagoreice. Concentrarea elevilor trebuie să aibă loc asupra alegerii corecte şi a folosirii noilor formule de arie, plus asupra calculului. Atrag astfel atenţia că aceasta este o lecţie pentru toţi elevii, construită deci cât mai accesibil, în organizarea lecţiilor, calculele cu situaţii iraţionale urmând să apară doar ulterior.
Prin această formă de organizare, eu cred că am găsit un echilibru onorabil între matematica-proces (destul de mare consumatoare de timp) şi matematica-rezultat (ca formă cristalizată şi eficientă temporal). Tot ce-aţi văzut aici s-a întâmplat în cca. 4 ore, la care trebuie să adăugăm jumătatea de oră de la început (recapitularea şi completările din clasa a 5-a). Ţinând cont că se adresează mai tuturor elevilor, eu cred că merită din plin. C. Titus Grigorovici
*
Apendix by Zara Hola: Citind articolul, m-au năpădit amintirile acestei lecții de când mi-a fost predată de către domnul profesor, în urmă cu doi ani. Acum, în clasa a noua fiind, am conștientizat dedesubturile valoroase ale lecției și importanța procesului ce precede rezultatul. Cu alte cuvinte, preocuparea acestei lecții reprezintă percepția ce ia loc conceptului. Lucrurile se prezintă elevului așa cum apar, ci nu cum sunt cristalizate. De-abia apoi apare fixarea relevantă a noțiunilor matematice, posibilă fiind apoi repetarea și memorarea lor. Această lecție pornește de la fapte și ajunge la concepte. Mai întâi matematica-proces, apoi matematica-rezultat.
Într-o altă ordine de idei, matematica-proces, în esență, cultivă indivizi care reflectă asupra problemei, cu o înțelegere solidă, transformându-i în creatori de cunoștințe. În contrast, matematica-rezultat, deși esențială, riscă să limiteze, putând să producă executanți pricepuți însă nu neapărat independenți, concentrându-se strict pe aplicarea unor formule și tehnici predefinite. Prin ochii mei, a unui elev mediocru la matematică, însă ce și-a însușit ariile figurilor de bază prin această lecție, știindu-le și la această oră, pot a spune aceea că, această lecție, prezentată în acest fel, este creată pentru a optimiza parcursul de învățare al elevului, ordinea pașilor fiind gândită astfel încât să respecte ritmul natural de asimilare al informațiilor noi de către elev. O capodoperă din punct de vedere al artei predării matematicii.



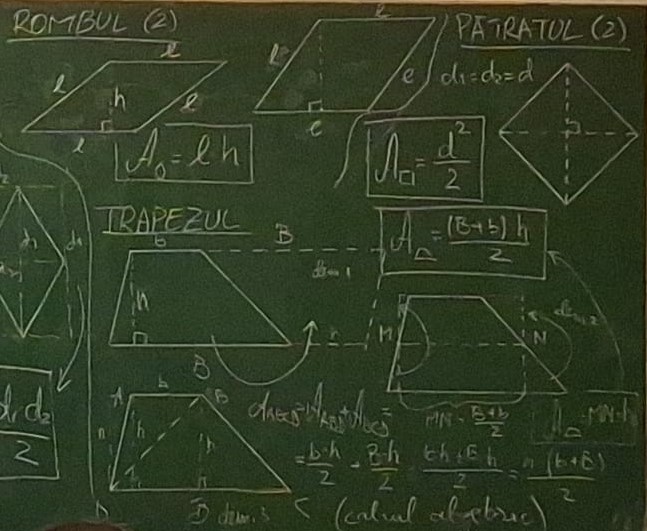

Iată calea de urmat în reforma predării-îvăţării matematicii!…Construcţia trebuie să fie baza deducţiei[